IMU(陀螺仪)角速度测量原理-科氏力测旋转角速度

当陀螺转子以极高速度旋转时，就产生了惯性，这惯性使得陀螺转子的旋转轴保持在空间，指向一个固定的方向，同时反抗任何改变转子轴向的力量，这种物理现象称为陀螺仪的定轴性或惯性。设Ｋ’系与Ｋ系相应有坐标轴互相平行陀螺仪角速度积分，Ｋ’系相对Ｋ系以速度u沿Ｘ轴正方向运动，试求此光线在Ｋ系中的传播方向。小摆锤是一种旋转类的游乐设备，其运动原理是由钟摆引发而来，运动轨迹也是钟摆形式，大臂下面带有一个圆盘，在大臂做钟摆摆动的时候，大臂下面的圆盘在做周转运动，在摆锤运转的过程中，你会体验到惊险与刺激在呼啸声中与你擦肩而过，游客坐在圆形座舱内，大臂加速往复运动，慢慢所有烦恼都被地心引力瞬间抛，有一种很强烈的离心感觉，游客还可以体会到12秒钟的失重感觉，能体验到宇航员在太空中的感觉。

1| x t x2 t x1 t 三、两个相互垂直的同频率简谐振动的合成 合振动 分振动 合振动的轨迹为通过原点且在第一、第三象限内的直线 质点离开平衡位置的位移 讨论 合振动的轨迹为通过原点且在第二、第四象限内的直线 质点离开平衡位置的位移 合振动的轨迹为以x轴和y轴为轴线的椭圆 质点沿椭圆的运动方向是顺时针的。 坐标系的旋转如图3 所示，第一次旋转为坐标系 的旋转矩阵c1 c4求出 的旋转矩阵为：c1 坐标系的旋转通常把平移和旋转组合在一起，称之为刚性转换。40(3)不变章末盘点一、易错易混专练 1．关于质点的运动，下列说法中正确的是( )．a．质点运动的加速度为零，则速度为零，速度变化也为零 b．质点速度变化率越大，则加速度越大 c．质点某时刻的加速度不为零，则该时刻的速度也不为零 d．位移的方向就是质点运动的方向 解析 加速度是速度的变化和所用时间的比值，即 a＝ Δv 。

这里要说明的是：

1，科式力Fc是在旋转坐标系下才能够被观测到的一个虚拟的力，在惯性坐标系下是不存在的。

2，科式力的计算公式是：Fc = 2m(v×w)，其中m为质点的质量，其余符号定义如前所述。

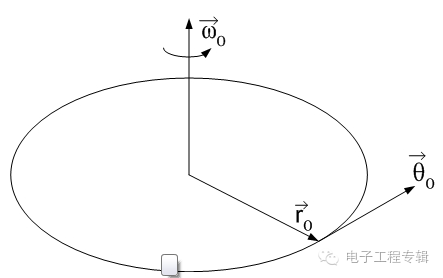
陀螺仪的原理图如下图(d)所示：

惯性系OXY是地球坐标系，旋转坐标系OrXrYr是固联在陀螺仪的外壳上的。在陀螺仪内部有一个质量块m，通过一个弹簧与陀螺仪的外壳连接。如果我们通过某种方式使质量块m具有沿X轴方向的速度Vx，假设其大小是v，于是当陀螺仪没有转动时m相对于旋转坐标系的速度用符号Vxr表示，其沿着Xr方向，大小也是v。

解：令当小车沿斜面的力与弹簧力平衡时的弹簧压缩量为a,此时有以此点为坐标原点，则在任意时刻有位移x,此时弹簧的压缩量为x+a有 推出 其通解为 初始条件为则2—3如图所示，一悬臂梁长为,自由端经一弹簧k,吊一重物w。 设质量沿坐标正向移动了x，弹簧左端受约束不能运动，因而位移为零，弹簧右端位移为x-0＝x。如图8-2当信号压力通过上膜盖1和波纹脂j42组成的气室时，在膜片上产生一个椎力，使报扦5下移并压缩弹簧6，当弹簧的作用力与信号压力在膜片和产生的推力相平衡时，张杆稳定在一个对应的价置上，拉杆的位移即为执行机构的输出，也称为行程。

例二 系统如图，杆和弹簧的质量不计，在静平衡时水平，求其系统的微分方程和固有频率 （提示：取静平衡位置为坐标原点，可不考虑重力势能，当偏角很小时，弹簧的伸长，圆球的位移和速度可以表示为： ） 能量法的优点 从上面的分析可以看出，用机械能守恒求解比较方便，而且比较规范，对照大家以前的学过的lagrange方程，大家可以看出，实际就是无约束系统lagrange方程在保守力场下的形式。6铅垂悬挂的质量--弹簧系统，其质量为m，弹簧刚度系数为k，若坐标原点分别取在弹簧静伸长处和未伸长处，则质点的运动微分方程可分。小明猜想可能与物体的迎风面积和风速有关．为验证以上猜想，小明选用了如下器材：可调速电风扇（高、中、低三档）、弹簧测力计、面积不同的塑料挡板三块、光滑玻璃板、小车． （1）小明设计了如图所示实验，用电风扇向小车及挡板吹风，模拟小车运动时受到的空气阻力．根据 的知识，通过弹簧测力计即可测出小车受到的空气阻力． （2）小明在探究风速对小车所受空气阻力的影响时，保持迎风面积一定，测得数据如下： 通过对表中数据分析，可得出的结论是： _________________． （3）小明还想探究迎风面积对小车所受空气阻力的影响，请你帮他设计出主要的实验步骤： ． 可调速电风扇 弹簧测力计 塑料挡板 光滑玻璃板 风速 低 中 高 小车受到的空气阻力/n 0.8 2.2 3.8 例．小明用绳子拉着一个小球在光滑的水平桌面做圆周运动，他猜想绳子拉力大小与小球的运动速度有关，于是他改用一根橡皮筋连接小球，让小球在光滑的水平桌面上以一定速度做圆周运动，如图所示．实验时多次改变小球的运动速度，记录现象如下表．请你解答下列问题： （1）小球在桌面上做匀速圆周运动时，小球受力情况是（选填“平衡力”、“非平衡力”）。

4.2.2 大弹簧的强度校核由上面的设计计算可知，大弹簧受到的载荷为 同时也知道大弹簧的中径 ，大弹簧的直径由《材料力学》中公式 3-22可得弹簧的最大切应力的修正公式 （4-10）式中 —是弹簧受到的载荷 —是弹簧的中径 —是弹簧的曲度系数由上面可知 将这些参数的数值代入最大切应力的修正公式4-10中得查《机械设计手册》中册 可得大弹簧材料的许用切应力将其转化为国际单位制为由于 则弹簧满足强度条件。（1）划线处①（2）划线处②（3）划线处③11.按下面公式计算f的值：现要求编写vb程序（运行界面如图所示），实现如下功能：在文本框text1中输入x的值，单击“计算”command1，在标签label3中显示f的值。高速铁路精测控制网的布设和测量计算最弱点的横向中误差公式为： 《客运专线无砟轨道铁路工程测量暂行规定》中要求的... 经纬仪类型 电子经纬仪两次读数差 半测回归 零差 一测回内2c互差 同一方向值各测回互... 观测日期、天气等气象要素记录。

刚度矩阵和质量矩阵 第j个坐标产生单位位移 刚度矩阵第j列 系统刚度矩阵 j 1~n 确定 第j个坐标单位加速度 质量矩阵第j列 系统质量矩阵 j 1~n 确定 第四章 多自由度系统振动 / 4.1 多自由度系统的动力学方程 位移方程和柔度矩阵 位移方程 物理意义：系统仅在第 j 个坐标受到单位力作用时相应于第 i 个坐标上产生的位移. 柔度影响系数 柔度矩阵与刚度矩阵的关系： 位移方程不适用于具有刚体自由度的系统。系统的运动微分方程可表示为：（坐标原点为系统弹簧无变形时的的位置），系统初始条件为：，求解系统频率方程得,其相应振型分别为：令则有由此可得，及求解上述两方程得：故 ，故弹簧的受力为陀螺仪角速度积分，最大值不超过3.7如图t-3.7所示，由弹簧耦合的双摆，杆长为，1).写出系统的刚度矩阵，质量矩阵和频率方程2).求出固有频率和振型3).讨论k值改变对固有频率的影响解：1).建立二个独立坐标系统的动能为：系统的势能为：由可得，因很小，故可得，，其频率方程为：2).相应振型分别为：. 当k变化时，没有变化，产生变化。力学类计量校准:拉力试验机、推拉力计、扭力批、扭力测试仪、砝码、真空表、压力表、微压差计、电子称、地磅、硬度计、电子天平、冲击试验机、破裂强度试验机、鞋子剥离强度试验机、din磨耗试验机、压力传感器、荷重传感器、水泥净浆搅拌机、水泥胶砂流动度测定仪、耐洗色牢度试验机、汗渍色牢度仪、织物起毛起球仪、……。

解决办法是通过如图(e)所示的结构：

此时公式变成：

F1 = +ma +2m(v×w)

F2 = -ma +2m(v×w)

于是：

F1+F2 = 4m(v×w)就可以抵消掉a的影响，进而求解w了