对数函数教案下载( 初一语文教案综合实践教学设计日益富强的祖国教学简笔画)

2019-2020高中数学222《对数函数及其性质》教学计划、中学语文教学计划、综合实践活动课堂教学设计、日益繁荣的祖国教学设计教学简笔画教学计划、牛津英语上海版教学计划,教案A,必修1个。教学目标 1. 知识与技能 ①对数函数的概念 熟悉对数函数的形象和性质规律 ②掌握对数函数的性质 能初步运用性质解决问题,乘法,口算100题,七年级有理数混合计算100题,电脑一级题库,二元线性方程组词题真话大冒险2.过程与方法二重积分的计算方法84消毒液的配比方法愚人节全人法现金流表编制法 数列求和的七种方法 让学生通过观察对数函数的形象来发现和总结对数函数 性质 3.情绪、态度和价值观①培养学生对数与形相结合的思维以及分析推理能力②Cul激发学生严谨的科学态度 二.学习方法和教学工具 1. 学习方法让学生观察、思考、交流和讨论功能的本质。教学方法多媒体计算机辅助教学。三。教学重点和难点 1. 重点理解对数函数的定义。掌握对数函数的形象和性质。 2. 难度。基数a对图像的影响以及对数函数属性的作用。四、教学过程 1. 设置 2.2.1 中的情况。在2.2.1的例6中,考古学家用来估计出土文物或古遗址的年代。对于每一个C14内容P,都有一个唯一确定的年龄与之对应,通过关系表达式。同样,每个对数公式中的任何正实数值都有一个对应于所有函数的唯一值。 2. 探索新知识。一般我们称一个函数>0且≠1为对数函数,其中自变量函数的定义域为0∞
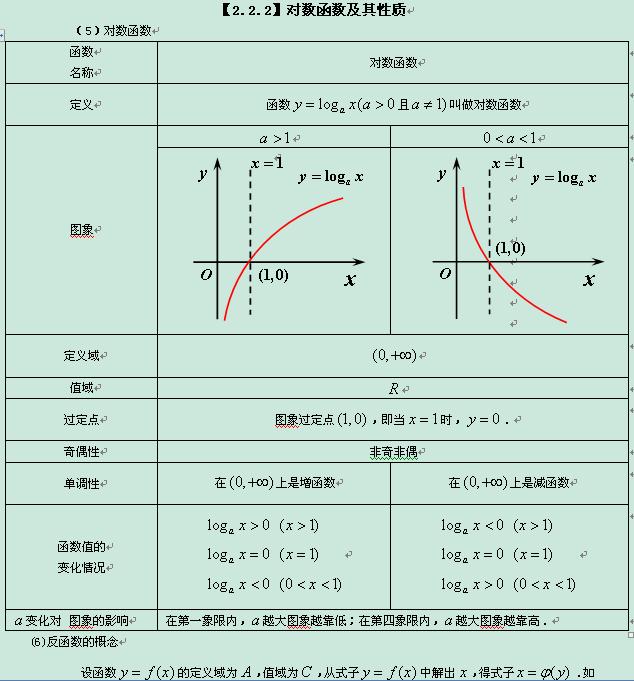


。问题1、为什么在函数定义中需要限制>0且≠1.2。为什么对数函数的域>0且≠1是0∞。组织学生充分讨论交流,使学生理解对数函数的含义,深化对数函数的理论求解。 ①根据对数与指数的关系可知,指数的概念必须定义才有意义。成本管理条例规定了对老年人的支持。法律规定妇女节放假规定3月8日放假规定鞋类三包>0且≠1。 ②因为无论取什么值都可以归结为指数函数的性质>0。例 1 求下列函数 12>0 且≠1 的定义域。从对数函数>0>0的定义分析。求解不等式以找到域。解1 因为>0表示≠0,函数的定义域为2,因为>0表示<4,所以函数的定义域为<我们研究函数的图像,利用图像研究函数的性质。首先完成P81表。维权者核对条目数及毫米对照表教师职称等级表员工考核分数表一般年金现值系数表2-3并根据该表用点法或用电脑绘制函数再用电脑软件绘制124681216-101225833584y0x 注意如果点的图像在图像上,点的图像是关于轴对称的,所以图像和图像是关于轴对称的。所以,我们能画出来的形象,首先是学生自己画出来的。电脑软件绘制



图像探索并选取了基数>0且≠1的几个不同的值,使对应的对数函数图像在同一平面直角坐标系中。观察图像,你能找出它们有什么特点吗?如何使用多媒体通过功能的图像进行绘图和提问。你能说出函数的基数和图像之间的关系吗?函数的图像有什么特点和属性?教师引导交流,总结功能性质。投影图像特征函数的性质。 1 图像位于轴的右侧。域为 0∞。 2 函数图像通过 10 个点。 21的对数为03。>1,图像逐渐上升,0<<1,图像逐渐下降,3>1,为增函数,0<<1,为减函数 4 >1,函数图像在10点的纵坐标右侧 如果大于0,则10点左侧的纵坐标小于0。当0<<1时,图像正好相反。 10点右边的纵坐标小于0 10点左边的纵坐标大于04 当>1>1则>00<<1<0 当0<<1>1则< 00<<1<0 从上表可知,对数函数的性质如下。首先,学生模仿指数函数的性质,完成老师的适当启发和引导>10<<1图像属性1域0∞2值域R3在10点上对数函数教案下载,即104为0∞处的增函数, 0∞ 是一个递增函数的例子


训练1 比较以下组数123>0和≠1的两个值。分析结合数字和形状的方法或利用函数的单调性完成1解。 1 使用图形计算器或多媒体绘制对数。在函数的图像中,图像上横坐标为34的点低于横坐标为85的点,因此解2是函数的单调递增函数,34<85,所以解3直接计算为一个计算器得到 2 的第二小 问题类似于 3 注意基数是一个常数,但要分类和讨论的范围则由函数的单调性决定。解 1 当> 1 时,它是 0 + ∞ 和 51 <59 上的增函数,所以当 1 是 0 + ∞ 和 51 <59 上的减函数时,所以解 2 转化为指数函数,单调指数函数的判断不同。顺序是当>1时,是R上的递增函数,51<59所以<即0<<1时,是R上的递减函数,51>59,所以
教案网123
为了国家稳定