2019-2020年高三数学总复习对数函数教案理教材分析

2019-2020年高三化学总复习对数函数教案理课本分析对数函数是一类重要的方程建模，它与指数函数互为反函数．教材是在教师学过指数函数、对数及其运算的基础上采用对数函数的概念的．须要说明的是，这里与特色的教材有所不同，即没有先学习反函数，这对学生学习对数函数的概念、图像及性质有较大影响，使指数函数的知识点不能直接应用于对数函数的知识点，但从对数的定义中了解：指数式与对数式可互化．因此，在这些方面，如在画对数函数y＝log2x的图像列表时，可以把画指数函数y＝2x图像时列的表中的x与y的值对调．这节内容的重点是对数函数的概念、图像及性质，难点是对数函数与指数函数的关系．教学目标1.通过详细例子，直观认识对数函数模型塑造的数量关系，初步理解对数函数的概念，并可画出准确对数函数的图象，掌握对数函数的图像跟性质．2.知道指数函数y＝ax与对数函数y＝logax互为反函数（a＞0且a≠1）．3.能应用对数函数的性质解有关问题．任务分析首先复习指数函数、对数的定义及对数的性质，这只是学习本节内容的基础．解析式x＝logay是变量，叫作对数函数，为了符合习惯，常写成y＝logax．这些内容学生较难理解，教学时应导致重视．教学中，要切记从例子出发，使学生从感性认识提

高到理性认识；要留意运用对比的方式；要结合对数函数的图象抽象概括对数函数的性质．注意：不规定讨论形式化的变量定义，也不规定求已知变量的反函数，只须知道对数函数与指数函数互为反函数．教学设计一、问题情境同指数函数中的细胞分裂问题，即：某种细胞分裂时，由1个分裂成2个，2个分裂成4个，4个分裂成8个……1个这样的细胞分裂x次后，得到的细胞的个数为y．我们将要知道，个数y是分裂次数x的方程，解析式是y＝2x．形式上是指数函数（这里的定义域是N）．思考：在这个难题中，细胞分裂的数量x是不是细胞分裂个数y的变量？若是，这个方程的解析式是哪个？x也有y的变量，由对数的定义得到这个新变量是x＝log2y．其中，细胞的个数y是自变量，细胞分裂的次数x是变量．二、建立建模1.学生讨论（1）函数x＝log2y与指数函数y＝2x有何关系？（2）函数ｘ＝log2y中的自变量、字母与我们曾经所学的函数有何差别？结论：问题（1）：两函数中的x表示的都是细胞分裂的数量，y表示的都是细胞分裂的个数，对应法则都是以2为底数，一个是取对数，一个是取指数，正好相逆．注意：这里不能说它们互为反函数，因为还没有学习反函数的概念．问题（2）：这里的自变量所用字母是y，以前学习的变量的自变量常用

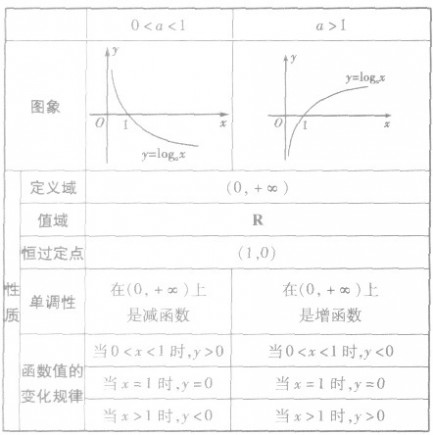
字母x，即此处的用法不合习惯．2.教师明晰定义：函数x＝long2y，（a＞0，且a≠1）叫作对数函数，它的定义域是（0，＋∞），值域是（－∞，＋∞）．由对数函数的定义可知，在指数函数y＝ax和对数函数x＝logay中对数函数教案下载，x，y两个变量之间的关系是一样的．不同的也是在指数函数y＝ax里，x是自变量，y是因函数，而在对数函数x＝logay中，y是自变量，x是因函数．习惯上，我们常用x表示自变量，y表示因函数，因此，对数函数通常写成y＝logay，（a＞0且a≠1，x＞0）．3.练习在同一坐标系中画出以下方程的图像．（1）y＝long2x．（2）y＝．解：列表：表12-1思考：上表中的x，y的对应值与指数函数中所列表的对应值有何关系？描点，画图：4.观察上面的变量图像，结合列表，仿照指数函数的性质，归纳总结出对数函数的性质（1）定义域是（0，＋∞），值域是（－∞，＋∞）．（2）函数图像在y轴的左侧且过定点（1，0）．（3）当a＞1时，函数在定义域上是增函数，且当x＞1时，y＞0；当0＜x＜1时，y＜0．当0＜a＜1时对数函数教案下载，函数在定义域上是减函数，且当x＞1时，y＜0；当0＜x＜1时，y＞0．三、解释应用［例题］1.求以下方程的定义域．（1）y＝log

2x2．（2）y＝loga（4－x）．（3）y＝．解：（1）｛x｜x≠0｝．（2）（－∞，4）．（3）（0，1）．2.比较下列各组数的大小．（1）log23与log23.5．（2）loga5.1与loga5.9，（a＞0且a≠1）．（3）log67与log76．解：（1）考查对数函数y＝log2x．∵2＞1，∴它在（0，＋∞）上是增函数．又3＜3.5，∴log23＜log23.5．（2）当a＞1时，loga5.1＜loga5.9；当0＜a＜1时，loga5.1＞loga5.9．（3）log67＞1＞log76．总结：本例是运用对数的单调性比较两个对数的大小，当底数与1的大小不确定时，要分类讨论；当不能直接进行非常时，可在两个数中间插入一个已知数间接比较两个数的大小．3.溶液的酸碱度是借助pH值来塑造的，pH值的推导公式为pH＝－lg［H+］，其中［H+］表示溶液中氢离子的含量，单位是mol／L．（1）根据对数函数性质及上述pH值的估算公式，说明氯气的酸碱度与氨水中氢离子的含量之间的差异关系．（2）已知纯净水中氢离子的含量为［H+］＝10-7mol／L，计算纯净水的pH值．解：（1）根据对数的性质，有pH＝－lg［H+］＝lg［H+］－

1＝lg，所以溶液中氢离子的含量越大，溶液的浓度就越小．（2）当［H+］＝10-7时，pH＝－lg10-7＝7，所以，纯净水的pH值是7．4.设函数f（x）＝lg（ax－bx），（a＞1＞b＞0），问：当a，b满足什么关系时，f（x）在（1，＋∞）上恒取正值？解：当x∈（1，＋∞）时，lg（ax－bx）＞0恒成立ax－bx＞1恒成立．令g（x）＝ax－bx．∵a＞1＞b＞0，∴g（x）在（0，＋∞）上是增函数，∴当x＞1时，g（x）＞g（1）＝a－b，∴当a－b≥1时，f（x）在（1，＋∞）上恒取正值．［练习］1.求方程y＝的定义域．2.比较log0.50.2与log0.50.3的大小．3.函数y＝lg（x2－2x）的增区间是____________．4.已知a＞0，且a≠1，则在同一直角坐标系中，函数y＝a-x和y＝loga（－x）的图像有也许是（）．5.大西洋鲑鱼每年都要逆流而上xxm，游回产地产卵．研究鱼类的科学家发现，一岁鲑鱼的游速可以表示为函数，单位是m／s，其中Q表示鲑鱼的耗氧量．（1）当一条鲑鱼的耗氧量是2700个单位时，它的游速是多少？（2）计算一条鲑鱼的最低耗氧量．四、拓展延伸1.作出对数函数y＝logax，（a＞1）与y＝l

ogax，（0＜a＜1）的草图．2.说出指数函数与对数函数的关系．以指数函数y＝2x与对数函数y＝log2x为代表加以说明．（1）对数函数y＝log2x是把指数函数y＝2x中自变量与因函数对调位置而得出的．教师明晰：当一个函数是一一映射时，可以把这个函数的因变量成为一个新的方程的自变量，而把这个方程的自变量作为新的方程的因函数．我们称这两个函数互为函数．函数y＝f（x）的反函数记作：y＝f-1（x）．对数函数y＝log2x与指数函数y＝2x互为反函数．（2）对数函数y＝log2x与指数函数y＝2x的图象关于直线y＝x对称．（3）指数函数与对数函数对照表．表12-2点评这篇案例首先借助细胞分裂问题表明了对数函数的涵义，这样安排既有利于学生理解对数函数的概念，又有利于学生认识了它与指数函数的关系．其次通过画具体的对数函数的图象，归纳总结出对数函数的性质，体现了由特殊到通常的了解规律，知识传授较为自然．性质的列出模仿了指数函数的性质．通过对比，便于学生理解、记忆．例题、练习的选配注意了题目的代表性，并且由易到难，注重学生解题能力的提升．拓展延伸侧重于指数函数与对数函数的图象、性质方面的关系，加深了学生对这两个函数的理解，并让学生从中了解了反函数的概念．