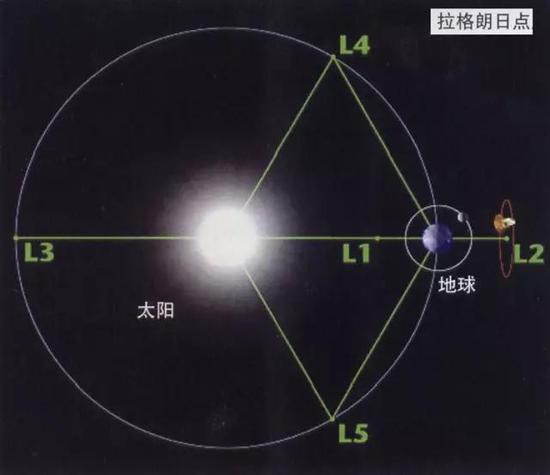
拉格朗日对偶性

专栏文章汇总
文章结构如下:
2: 对偶问题
3: 原始问题和对偶问题的关系
4: 参考文献
除了用解决qp问题的常规方法之外,还可以通过求解对偶问题得到最优解,这就是线性可分条件下支持向量机的对偶算法,这样做的优点在于:一者对偶问题往往更容易求解。现在要对凸优化进行求解,现在给出的经验求解方法是,通过求解对偶问题得到最优解。虚拟盘转文件夹导致的同步问题3.解决托盘状态和云桥面板状态有时不统一的问题4.定时同步支持在某个时间段内同步5.在全屏模式下不会弹出气泡通知6.发送文件到快盘支持选择存放目录7.优化频繁保存时容易冲突的问题2.10.30.7 更新日志1.加快查找文件变化速度2.降低对开机速度的影响3.优化冲突文件处理逻辑4.解决签到慢的问题5.解决某些情况下文件会同步到根目录的问题6.支持定时同步。
对偶问题有非常良好的性质,以下列举几个:
对偶问题的对偶是原问题;
无论原始问题是否是凸的,对偶问题都是凸优化问题;
对偶问题可以给出原始问题一个下界;
当满足一定条件时,原始问题与对偶问题的解是完全等价的;
1. 单位冲击函数 δ t 的定义 通常单位冲击函数 δ t 可定义如下: ∞ t 0 δ t 2 .6 .1 0 t≠0 ε且 ∫δ t d t 1 , 对任意 ε 0 2 .6 .2 - ε 对于任意函数 Φ t , 有 b b Φ t δ t - t d t Φ t δ t - t d t ∫ 0 ∫ 0 a a Φ t 若 a t b, 且 Φ t 在 t t 连续 0 0 0 2 .6 .3 0 若 t0 a , b ·12 · 第二章 确定信号分析 δ t 函数可 以看作是某种函数的极限。定义在某个开区间c内的凸函数f在c内连续,且在除可数个点之外的所有点可微.如果c是闭区间,那么f有可能在c的端点不连续. 一元可微函数在某个区间上是凸的,当且仅当它的导数在该区间上单调递减. 一元连续可微函数在区间上是凸的,当且仅当函数位于所有它的切线的上方:对于区间内的所有x和y,都有f(y) ≥ f(x) + f '(x) (y −。中支持内联函数,其目的是为了提高函数的执行效率,用关键字 inline 放在函数定义(注意是定义而非声明,下文继续讲到)的前面即可将函数指定为内联函数,内联函数通常就是将它在程序中的每个调用点上“内联地”展开,假设我们将 max 定义为内联函数:。
称约束最优化问题
为原始最优化问题或原始问题。
首先引入拉格朗日函数(generalized Lagrange function)
其中, 是拉格朗日乘子,
。
构建关于 的函数
假设给定某个违反原始问题约束条件的 ,即存在某个
使得
或
。若
,可令
,使得
;若
,可令
使
,使得
。将其余
均取值为0。
即
假设给定某个符合原始问题约束条件的 ,即
且
,
则
由以上,得
则极小化问题
与原始最优化问题等价拉格朗日 对偶,即有相同的解。(因为当趋向无穷时,问题无解,因此必须满足约束条件)
称为广义拉格朗日函数的极小极大问题。
定义原始问题的最优值

称为原始问题的值。
构建关于 的函数
则极大化问题
称为广义拉格朗日函数的极大极小问题。
将广义拉格朗日函数的极大极小问题表示为约束最优化问题
称为原始问题的对偶问题。
定义对偶问题的最优值
称为对偶问题的值。

若原始问题与对偶问题都有最优解,则
这个性质便叫做弱对偶性(weak duality),对于所有优化问题都成立,即使原始问题非凸。
与弱对偶性相对应的有一个强对偶性(strong duality) ,强对偶即满足:
由于原问题和对偶问题均有可行解,根据弱对偶性的推论,原问题(极大化问题)的目标函数值具有上界,而对偶问题(极小化问题)的目标函数值具有下界,因此不可能具有无界解的情况,而且“可行解”的前提也保证了没有无解的情况,所以两者都一定具有最优解。存在两者的可行解,使得原问题和对偶问题的的目标函数值相等,由对偶问题的最优性,这时令两者的目标函数值相等的可行解均为最优解,即此时原问题和对偶问题它们最优解下的目标函数值相等。理解温度场、等温面线、温度梯度和热流密度等基本概念的物理意义 傅立叶定律是导热的重要定律熟悉它的物理意义、数学表达式及其应用 了解直角坐标系常物性物体导热微分方程的推导过程理解导热微分方程中各项物理意义写出给定的简单导热问题的完整数学描述导热微分方程和定解条件会由导热微分方程和定解条件求解第一类边界条件下常物性、无内热源的一维稳态导热物体内的温度场和导热量 掌握平壁和圆筒壁导热量以及多层壁界面温度的计算 理解热导系数随温度线性变化时导热问题的处理方法并能用试算法求解这类导热问题。
Slater条件:对于原始问题及其对偶问题,假设函数 和
是凸函数,
是仿射函数,且不等式约束
是严格可行的,即存在
,对所有
有
,则存在
,使
是原始问题的解,
是对偶问题的解,并且
也就是说如果原始问题是凸优化问题并且满足 Slater 条件的话,那么强对偶性成立。需要注意的是拉格朗日 对偶,这里只是指出了强对偶成立的一种情况,并不是唯一的情况。
KKT条件:对于原始问题及其对偶问题,假设函数 和
是凸函数,
是仿射函数,且不等式约束
是严格可行的,即存在
,对所有
有
,则存在
,使
是原始问题的解,
是对偶问题的解的充分必要条件是
满足下面的Karush-Kuhn-Tucker(KKT)条件:
总的来说就是说任何满足强对偶性的优化问题,只要其目标函数与约束函数可微,任一对原始问题与对偶问题的解都是满足 KKT 条件的。即满足强对偶性的优化问题中,若 为原始问题的最优解,
为对偶问题的最优解,则可得
满足 KKT 条件。
KKT详见:Karush-Kuhn-Tucker (KKT)条件
现在我们把对偶问题得出了,但怎么对偶问题进行求解呢。但是,从许多可以用贪心算法求解的问题中看到这类问题一般具有2个重要的性质:贪心选择性质和最优子结构性质。而求解这个对偶学习问题,分为3个步骤:1、让l(ω, b, α)关于ω 和 b 的最小化。
李航. 统计学习方法[M]. 北京:清华大学出版社,2012
支持向量机:Duality " Free Mind
太牛叉了