探究三角形的几何“重心”与物理“重心”
刘学禹��
在学习高一物理(必修1)《重力 基本相互作用》一节时,老师介绍了重心概念,所谓重心就是重力的等效作用点,重心的位置与物体的形状和质量分布情况有关.不过重心概念并非高中物理首次接触,早在初中《数学(八年级下)》教材中,我们就曾学习到三角形的重心,所谓三角形的重心乃三角形的三条中线的交点.由此,我产生一个疑问:物理学中的重心与几何学上的重心是否一致?具体地说,三角形的物理重心与几何重心是否重合?这个问题一直困扰着我,经过一年多的思考和探究,有了一点不成熟的想法,现把它写出来,请老师们批评指正.
本文所讨论的三角形分两种情形,一是质量均匀分布、粗细一致的三角形(空心)线框;二是质量均匀分布的三角形薄板.对于第一种情况,我发现三角形线框的物理重心与其几何重心通常并不重合;对于第二种情况,三角形薄板的物理重心与其几何重心的确完全一致.
1初步验证
我通过实验进行了简单的验证:用一根长而粗的铁丝弯成一个每边长在20 cm-30 cm左右的任意三角形线框,并在这个三角形铁丝上蒙上保鲜膜(质量可忽略不计).然后用直尺作出这个三角形的几何重心(位于保鲜膜上).最后再用手指(食指)从下面顶着这个几何重心的位置,看能否把这个三角形铁丝悬空平顶支撑起来.结果发现即使在可以少许调整的情况下也无法将三角形铁丝支撑平衡起来.这说明三角形线框的几何重心与其物理重心并不重合.

再取了一块厚度相同的木板,把它锯成三角形,然后也用直尺作出这个三角形木板的几何重心.平放着木板,再用手指从下面顶着这个几何重心的位置,发现只要少许调整,手指确实可将木板水平悬空支撑起来而不倾倒掉落.这时木板只受重力和手指的支持力作用,是一对平衡力,说明其重心在手指尖所在的竖直线上,即三角形的几何重心与其物理重心重合!
改变三角形铁丝和三角形木板的形状,多次重复上述两个实验,结果基本一致.不过,我仍然不能完全满意,因为我发现不管怎么仔细完成上述实验,总要进行适当调整.实际上,对于第二个实验,不用手指,改用较细的铁钉,就难以水平支撑平衡起三角形木板.尽管这里存在木板质量是否均匀分布、用直尺作图确定几何重心位置是否准确等等干扰因素,误差在所难免,但实验的验证无论如何总难令人完全信服.于是我尝试从理论上探究这两个重心的关系.
2理论探究
2.1三角形空心线框的几何重心与其物理重心是否重合?
要否定这个命题,可以进行证伪.也就是说只要找到一个反例,即可得到证明.

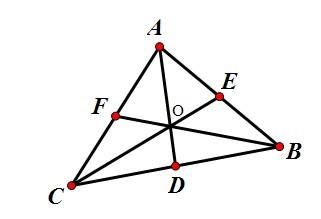
如图1所示,设质量、粗细均匀分布的三角形线框OAB的三条边长分别为OA=4、OB=3、AB=5,三角形处于图示的直角坐标系中.再设三条边单位长度的质量为λ,则三条边的质量分別为mOA=4λ、mOB=3λ、mAB=5λ.首先确定线框OAB的物理重心.由于三条边的质量均匀分布,所以可将AB边的质量等效集中于AB边的中点D,容易看出D点位置坐标为(1.5,2.0),等效质量为5λ;同理可将OB边、OA边的质量分别等效集中于OB、OA的中点E、F,位置坐标分别为(1.5,0)、(0,2.0),等效质量为3λ、4λ.接着再将D、E两点进行等效,D、E两点的重心位置M必在这两点的连线上,并且到D、E两点的距离与D、E两点的等效质量成反比.这样不难确定M点的位置坐标为(1.5,1.25)、等效质量为8λ.最后再考察M、F两点的重心G的位置,采用上述同样的方法,能够计算出G点的位置坐标为(1.0,1.5),它也是整个三角形线框的物理重心.
接下来再确定线框OAB的几何重心G′.根据三角形几何重心的性质——重心到顶点的距离与重心到对边中点的距离之比为2∶1,我们知道,△OAB的重心G′一定在中线OD上,并且满足OG′=2G′D.不难计算G
②充分利用几何图形的对称性. 2.求某点的坐标时,一般先找这一点在某一坐标平面上的射影,确定其两个坐标,再找出它在另一轴上的射影(或者通过它到这个坐标平面的距离加上正负号)确定第三个坐标. (2015·广州模拟)如下图所示,已知正四面体a-bcd的棱长为1,e,f分别为棱ab、cd的中点. (1)建立适当的空间直角坐标系,写出顶点a,b,c,d的坐标. (2)求ef的长. [分析]正四面体也是正三棱锥,即其顶点和底面正三角形中心的连线是正四面体的高,以底面正三角形的中心为坐标原点,高为z轴,建立空间直角坐标系.。以顶点为基础,对几何图元进行处理,把三维坐标转变为二维屏幕坐标的过程。直线与圆的位置关系这一内容,蕴含着丰富的数学思想.首先,直线与圆的位置这一几何特征,是通过点的坐标和直线、圆的方程来研究,体现了数形结合的思想方法.这在学习直线的方程、圆的方程时,学生已经接触过,结合本节课内容,可以进一步加强对数形结合思想方法的理解,发挥从“数”和“形”两个方面共同分析解决问题的优势.其次,从本节课知识的研究过程来看,由“几何问题(位置关系)”到“代数问题(坐标、方程、点到直线的距离公式、联立方程组等),再到“几何问题(分析代数结果的几何含义)”,充分体现了由“形”到“数”,再由“数”到“形”的转化过程,是转化思想的具体应用.再有,通过具体例子判断直线与圆的位置关系,来归纳总结判断直线与圆位置关系的方法,充分体现了由特殊到一般的思想方法.。
【设计意图】通过问题的设计,不但可以巩固所学知识,还可以让学生真正体会由“几何问题(位置关系)”到“代数问题(坐标、方程、点到直线的距离公式、联立方程组等),再到“几何问题(分析代数结果的几何含义)”,充分体现了由“形”到“数”,再由“数”到“形”的转化过程,是转化思想的具体应用.。工程上常用的高程测量方法有几何水准测量、三角高程测量、gps测高及在特定对象和条件下采用的物理高程测量,其中几何水准测量是目前高程测量中精度最高、应用最普遍的测量方法。直线与圆的位置关系这一内容,蕴含着丰富的数学思想.首先,直线与圆的位置这一几何特征,是通过点的坐标和直线、圆的方程来研究,体现了数形结合的思想方法.这在学习直线的方程、圆的方程时,学生已经接触过,结合本节课内容,可以进一步加强对数形结合思想方法的理解,发挥从“数”和“形”两个方面共同分析解决问题的优势.其次,从本节课知识的研究过程来看,由“几何问题(位置关系)”到“代数问题(坐标、方程、点到直线的距离公式、联立方程组等),再到“几何问题(分析代数结果的几何含义)”,充分体现了由“形”到“数”,再由“数”到“形”的转化过程,是转化思想的具体应用.再有,通过具体例子判断直线与圆的位置关系,来归纳总结判断直线与圆位置关系的方法,充分体现了由特殊到一般的思想方法.。
2.2三角形薄板的几何重心与其物理重心是否重合?
这个问题相对复杂,下面先从两个简单的情况说起.
命题13个质量相等的小球分别位于三角形的顶点,则这3个小球的物理重心与该三角形的几何重心重合.
说明:如图2所示,容易理解A、B两球的重心位于AB的中点D.D(A、B两球的等效点)和C球的物理重心位于G,显然G点实际上也就是三个小球A、B、C的物理重心.由于D点的相当于集中了A、B两球的质量,所以GC的距离是GD的2倍.对照附注中三角形的(几何)重心性质2——三角形的(几何)重心到顶点的距离与(几何)重心到对边中点的距离之比为2∶1,不难看出G点也就是三角形ABC的几何重心.
命题2如果均质三角形线框的三条边的粗细(宽度)与其长度成反比,则三角形线框的物理重心与该三角形的几何重心重合.
说明:由于线框三条边的粗细(宽度)与其长度成反比,可知三条边的表面积(设线框的厚度一致)

相等,所以三条边的质量相等,如图3所示.加之三边的质量分布均匀,因而可以认为,三条边AB、BC、CA的质量分别集中于它们的中点D、E、F.再考察三角形DEF的物理重心,它与与命题1的情形完全相同.并且根据图3不难看出△ABC与△DEF的几何重心重合.所以△ABC线框的物理重心与△DEF的几何重心亦即△ABC的几何重心重合.最后再来探究均质三角形薄板的重心位置问题.如图4所示,令G点为薄板ABC的几何重心,连接AG、BG、CG.并将线段AG、BG、CG各自均分n等份,再将AG、BG、CG边上n等份的点分别顺次对应连接起来,这样便把整个△ABC分割成n个三角形空心线框.图4中实线所示的A1B1C1-A2B2C2为其中的一个三角形线框.
下面讨论三角形线框A1B1C1-A2B2C2的物理重心位置.根据附注中三角形的(几何)重心性质3——三角形的(几何)重心和三角形的三个顶点组成的3个三角形面积相等,即有S△ABG=S△BCG=S△CAG.在△ABG中,由于线段A1B1、A2B2…把△ABG分成n个细长的小梯形,这些小梯形的面积从顶
点G到底边AB按特定比例递增(不难理解,△BCG和△CAG中的情况也是一样).这样图4中三角形线框A1B1C1-A2B2C2的三条边A1B1B2A2(即图4中显示的细长的小梯形)、B1C1C2B2、C1A1A2C2的面积也相等.加之质量分布均匀,所以三角形线框A1B1C1-A2B2C2的三条边的质量相等.结合前述的命题2可知三角形线框A1B1C1-A2B2C2的物理重心就在G点.同理,其他三角形线框的物理重心也都在G点,所以整个三角形薄板的物理重心就在其几何重心G点上.
上述的证明实际上就是微元法,把三角形薄板分割成若干个三角形线框.这与高中物理必修1教材中推导匀变速运动的位移-时间关系x=v0t+12at2的思路类似.由此可见,高中的物理学习,方法比内容更为重要,这也是我在探索重心问题时得到的一点体会.
(指导老师:于正荣)
加速了中国造假业的发展