三角形的五心：内心、外心、重心、垂心、旁心，都在这了，全讲明白

3、中心：三角形只有五种心重心、垂心、内心、外心、旁心，当且仅当三角形是正三角形的时候，四心合一心，称做正三角形的中心。三角形的重心、外心、垂心、内心、旁心称为三角形的五心.它们都是三角形的重要相关点.。 (2) 利用 性质把行列式化为上三角 形行列式， 从而算得行列式的值．计算4阶行列式思考题1111b11b11a12222bbbbaaa 11d111c1c22222dddccd 1abcd 已知思考题解答解11b11a222aa11b11b11a12aa11d11c122ddccbbd 11d111c1c1222ddcbc1dc1dcb1b1ba1a1aabcd11111222c1dc1dcb1b1ba1a1a1111112223d1112d1112。

一.重心

三角形的三条中线的交点叫三角形的重心.

如图,设O为三角形的重心,则有

1.重心到顶点的距离与重心到对边中点的距离之比为2：1三角形重心位置。

2.重心和三角形3个顶点组成的3个三角形面积相等。

②充分利用几何图形的对称性． 2．求某点的坐标时，一般先找这一点在某一坐标平面上的射影，确定其两个坐标，再找出它在另一轴上的射影(或者通过它到这个坐标平面的距离加上正负号)确定第三个坐标． (2015·广州模拟)如下图所示，已知正四面体a－bcd的棱长为1，e，f分别为棱ab、cd的中点． (1)建立适当的空间直角坐标系，写出顶点a，b，c，d的坐标． (2)求ef的长． [分析]正四面体也是正三棱锥，即其顶点和底面正三角形中心的连线是正四面体的高，以底面正三角形的中心为坐标原点，高为z轴，建立空间直角坐标系．。重心的坐标是顶点坐标的算术平均数。（3）在（2）的条件下，求四边形的面积.28.（本小题满分12分）在平面直角坐标系中，已知抛物线（为常数）的顶点为，等腰直角三角形的定点的坐标为，的坐标为，直角顶点在第四象限.（1）如图，若该抛物线过 ，两点，求该抛物线的函数表达式。

4.重心和三角形3个顶点的连线的任意一条连线将三角形面积平分。 5.重心到三角形3个顶点距离的平方和最小。

6.重心是三角形内到三边距离之积最大的点。

7.重心在向量中的重要结论:外心

二.外心

三角形三边的垂直平分线的交点叫三角形的外心.(外接圆的圆心)

1.三角形的外接圆有且只有一个，即对于给定的三角形，其外心是唯一的，但一个圆的内接三角形却有无数个，这些三角形的外心重合。

2.锐角三角形的外心在三角形内；钝角三角形的外心在三角形外；直角三角形的外心与斜边的中点重合

4.OA=OB=OC=R

5.∠BOC=2∠BAC，∠AOB=2∠ACB，∠COA=2∠CBA

6.S△ABC=abc/4R

三.内心

三角形的内心是三角形三条角平分线的交点(或内切圆的圆心)三角形重心位置。

三角形的内心的性质

1.三角形的三条角平分线交于一点，该点即为三角形的内心

2.三角形的内心到三边的距离相等，都等于内切圆半径r

3.r=2S/(a+b+c) 4.在Rt△ABC中，∠C=90°，r=(a+b-c)/2．

5.∠BOC = 90 °+∠A/2 ∠BOA = 90 °+∠C/2 ∠AOC = 90 °+∠B/2

6.S△=[(a+b+c)r]/2 (r是内切圆半径)

四.旁心

1 三角形的一条内角平分线与其他两个角的外角平分线交于一点，该点即为三角形的旁心。

2旁心到三角形三边的距离相等。

3三角形有三个旁切圆，三个旁心。旁心一定在三角形外。

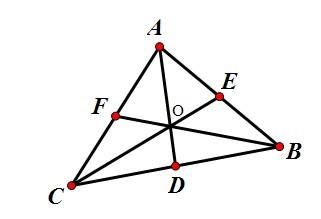
4直角三角形斜边上的旁切圆的半径等于三角形周长的一半。

5∠BI1C=90°-∠A/2.

6AP1=r1·cot(A/2)=(a+b+c)/2.

7∠AI1B=∠C/2.

8S⊿ABC=r1(b+c-a)/2.

9r1=rp/(p-a).

10r1=(p-b)(p-c)/r.

111/r1+1/r2+1/r3=1/r.

12r1=r/(tanB/2)(tanC/2).

五.垂心

三角形的垂心是三角形三边上的高的交点(通常用H表示)。

三角形的垂心的性质

1.锐角三角形的垂心在三角形内；直角三角形的垂心在直角顶点上；钝角三角形的垂心在三角形外

2.三角形的垂心是它垂足三角形的内心；或者说，三角形的内心是它旁心三角形的垂心

3. 垂心O关于三边的对称点，均在△ABC的外接圆上

4.△ABC中，有六组四点共圆，有三组(每组四个)相似的直角三角形，且AO·OD=BO·OE=CO·OF

5. H、A、B、C四点中任一点是其余三点为顶点的三角形的垂心(并称这样的四点为一—垂心组)。

6.△ABC，△ABO，△BCO，△ACO的外接圆是等圆。

46. 如果在两个三角形中，且一个的夹角大于另一个的夹角，而且三角形的三个内角的和等于二直角，则等角所对的边也彼此相等. 等底且在底的同侧的相等三角形也在相同二平行线之间，一个的两个角分别等于另一个的两个角. 如果一直线和两直线相交所成的错角彼此相等，它们表达相同的命题，命题是指一个判断的语义，且和直线所成邻角和等于二直角。 （3）设 t 的值分别取 t1、t2 时（t1≠t2） ，所对应的三角形分别为△af1p1 和△af2p2.试 判断这两个三角形是否相似，请证明你的判断. 29，操作：在△abc 中，ac＝bc＝2，∠c＝90° ，将一块等腰直角三角板的直角顶点 放在斜边 ab 的中点 p 处，将三角板绕点 p 旋转，三角板的两直角边分别交射线 ac、cb 于 d、e 两点.如图 20，21，22 是旋转三角板得到的图形中的 3 种情况. 研究： （1）三角板绕点 p 旋转，观察线段 pd 和 pe 之间有什么数量关系。1 过两点有且只有一条直线 2 两点之间线段最短3 同角或等角的补角相等 4 同角或等角的余角相等 5 过一点有且只有一条直线和已知直线垂直 6 直线外一点与直线上各点连接的所有线段中，垂线段最短 7 平行公理经过直线外一点，有且只有一条直线与这条直线平行 8 如果两条直线都和第三条直线平行，这两条直线也互相平行 9 同位角相等，两直线平行 10 内错角相等，两直线平行 11 同旁内角互补，两直线平行 12两直线平行，同位角相等 13 两直线平行，内错角相等 14 两直线平行，同旁内角互补 15 定理 三角形两边的和大于第三边 16 推论 三角形两边的差小于第三边 17 三角形内角和定理三角形三个内角的和等于180° 18 推论1 直角三角形的两个锐角互余 19 推论2 三角形的一个外角等于和它不相邻的两个内角的和 20 推论3 三角形的一个外角大于任何一个和它不相邻的内角 21 全等三角形的对应边、对应角相等 22边角边公理(sas) 有两边和它们的夹角对应相等的两个三角形全等 23 角边角公理( asa)有两角和它们的夹边对应相等的两个三角形全等 24 推论(aas) 有两角和其中。

8.三角形任一顶点到垂心的距离，等于外心到对边的距离的2倍。

9.设O，H分别为△ABC的外心和垂心，则∠BAO=∠HAC，∠ABH=∠OBC，∠BCO=∠HCA。

10.锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍。

锐角三角形的垂心是垂足三角形的内心。11.锐角三角形的垂心是垂足三角形的内心。锐角三角形的内接三角形中。