等腰三角形知识点及典型习题教案模板3(【每日一题】三角函数知识归纳与典型例题解析)
简介:
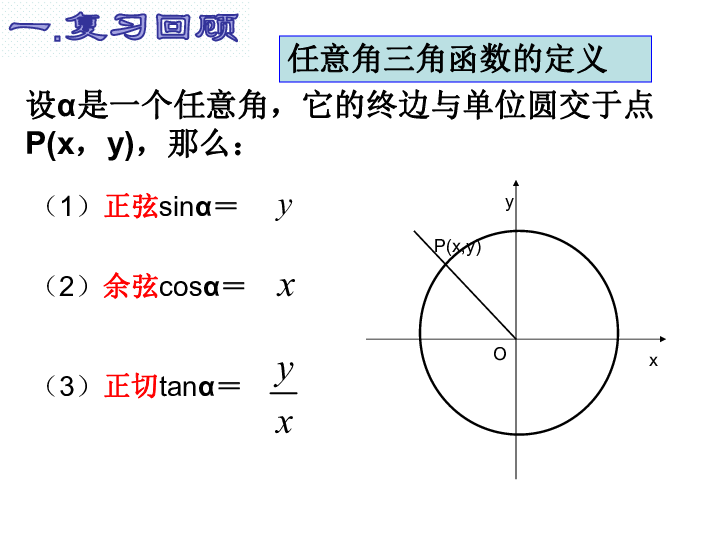
三角函数知识归纳及典型例子
1、Angle 概念推广:平面中的图形,其中光线围绕端点从一个位置旋转到另一个位置。逆时针旋转形成的角称为正角,顺时针旋转形成的角称为负角。当一条射线不作任何旋转时,就说它形成了一个零角。射线的起始位置称为起始边,结束位置称为终止边。
2、象限角的概念:在笛卡尔坐标系中,角的顶点与原点重合,角的起始边与轴的非负半轴重合,结束角的边在象限内,只说这个角就是象限的角。如果角的端点在坐标轴上,则认为该角不属于任何象限。
3.末尾相同角度的表示:
(1)端边与端边相同(端边在端边所在的射线上),注意:等角的端边必须相同,与相同的端边不一定相等。
例1.与角的端边相同,绝对值最小的角的度数为_,即_ _弧度。
(2)端边与端边共线(端边在端边所在的线上)。
(3)端边和尾边关于轴对称。
(4)端边和端边关于轴对称。
(5)端边和尾边关于原点对称。
(6)端边在轴上的角度可以表示为:;端边在轴上的角度可以表示为:;端边在坐标轴上的角度可以表示为: .
例2. 的端边和端边关于一条直线对称等腰三角形知识点及典型习题教案模板3,则=____________。
4、和的最终关系:由“每个象限的两半等腰三角形知识点及典型习题教案模板3,一、二、三、四”决定。
例3.如果是第二象限角,就是__一、三___象限角
5.弧长公式:,扇形面积公式:1弧度(1rad)。
例4.知道一个扇形AOB的周长是6厘米,扇形的中心角是1弧度,求扇形的面积。
答案:2)
6、任意角的三角函数定义:假设是任意角,P为终端边上任意一点(与原点不同),它与原点的距离为,则, ,,。三角函数的值只与角度的大小有关,与点P在终端边上的位置无关。
例5.(1)已知角的端点经过点P(5, -12),值为__。
(2)为第一个三、四象限角,取值范围为___(-1, ____.
(3)若,判断A的符号:否定
7.三角函数线的特点是:正弦线MP“立于轴上(起点在轴上)”,余弦线OM“立于轴上(起点为原点)” ”,切线AT“立点(起点是)”。三角函数线的重要应用是比较三角函数的值和求解三角不等式。
例6.(1)若,大小关系为_____()

(2)如果是锐角,大小关系是_______,()
(3)函数的定义域是_______,
答案:
8.特殊角度的三角函数值:
30°
45°
60°
0°
90°
180°
270°

15°
75°
1
-1
1
-1
1
2-
2+
1
2+

2-
9.同角三角函数的基本关系式:
(1)square关系:
(2)相互关系:sincsc=1,cossec=1,tancot=1,
(3)quotient 关系:
同角三角函数基本关系表达式的主要应用是知道一个角的三角函数的值,并求出这个角的其他三角函数的值。用平方关系解决问题时,需要根据已知角度的范围和三角函数的值,尽可能压缩角度的范围,从而确定符号;在三角函数值的具体计算中,一般不必使用同一个角三角形函数的基本关系表达式是先根据角的范围确定三角函数值的符号,然后用解直角三角形求三角函数值的绝对值。
例7.(1)函数值的符号为____大于0,
(2)If, 使其为真的取值范围是 ____ ,
答案:
(3)已知,则=___ ,
(4)已知,则=____;

=________ _;
(5)已知,等于(B)
A, B, C, D,;
(6)已知,值为______ -1。
10.三角函数归纳公式()的本质是:奇到偶不变(比如指奇数或偶数),符号看象限(看原函数,而同时也可以看作是一个锐角)归纳公式的应用是求任意角的三角函数的值。一般步骤:(1)负角变正角,然后写成2k+,;(2)成锐角三角函数。
例8.(1)的值为________;
(2)已知,然后___ ___,
如果是第二象限角,则______。
11、两角和差的正弦、余弦、正切公式和双角公式:
例9.(1)以下公式中,值为(C)
A, B, C, D,;
(2)定题P:,命题Q:,那么P就是Q()
A、充分必要条件 B、充分必要条件 C、充分必要条件 D、两者都... 更多>>
教案网123
照他的观点