Matrix67: The Aha Moments

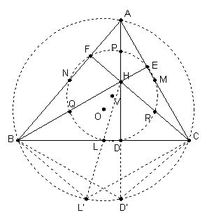
任意一个三角形的三条中线都会交于一点，这个点就叫做三角形的“重心”。任意一个三角形的三条高都会交于一点，这个点就叫做三角形的“垂心”。任意一个三角形三边的垂直平分线都会交于一点，这个点就叫做三角形的“外心”。 1765 年，大数学家 Euler 指出：任意一个三角形的重心、垂心和外心都在一条直线上，并且重心会把垂心和外心的连线分成 2 : 1 两段。这个结论虽然有很多很漂亮的证明，但作为一个非常基本的结论，它还有一种非常直观的解释方法。最近在做一个课件的时候，需要用到这种直观理解的动画演示，结果在网上找了半天也没找到，最终决定自己做了一个。

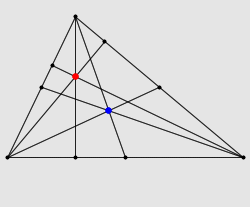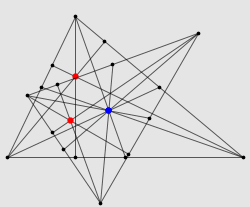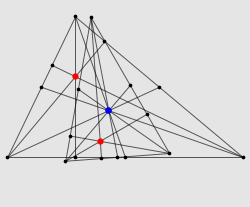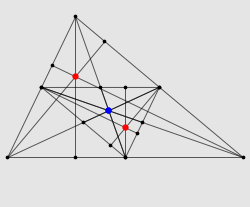
上图中，红色的点是三角形三条高的交点，也就是垂心；蓝色的点是三角形三条中线的交点，也就是重心。现在，把整个三角形绕着重心旋转 180 度，同时以重心为中心把图形缩小到原来的一半。于是，每个点都会跑到重心的正对面去，同时到重心的距离也会缩短到原来的一半。你会发现，由此得到的小三角形，三个顶点都在大三角形各边的中点处（因为它们是大三角形的顶点转过来得到的，而重心在各中线的 2 : 1 处）；同时三角形欧拉定理，小三角形的三条高分别与大三角形的各边垂直（因为它们是大三角形的高转了 180 度得到的）。你会发现，小三角形的垂心正好就是大三角形的外心！而小三角形的垂心就是由大三角形的垂心转过来得到的三角形欧拉定理，这两个点与重心应该在一条线上，并且到重心的距离有 1 : 2 的关系。这样一来，我们就相当于证明了 Euler 线定理。