反三角函数公式大全

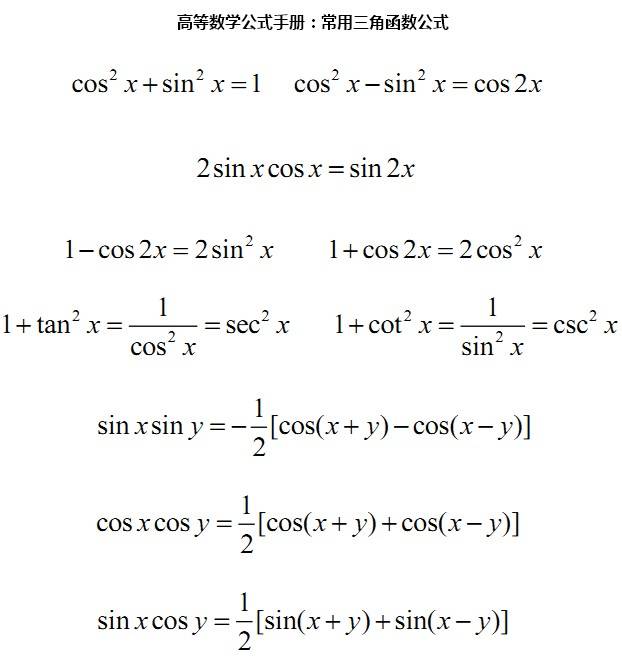
三角函数公式 两角和公式 sin(A+B) = sinAcosB+cosAsinB cos(A+B) = cosAcosB-sinAsinB tan(A+B) = cot(A+B) = 倍角公式 tan2A =2tanA 1 ? tan A2sin(A-B) = sinAcosB-cosAsinB cos(A-B) = cosAcosB+sinAsinBtanA ? tanB 1 ? tanAtanBtanA ? tanB 1 - tanAtanBtan(A-B) = cot(A-B) =cotAcotB-1cotAcotB?1cotB ? cotAcotB ? cotASin2A=2SinA?CosA Cos2A = Cos2A-Sin2A=2Cos2A-1=1-2sin2A 三倍角公式 sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosA tan3a = tana·tan( 半角公式 sin(A 2 A 2?3+a)·tan(?3-a))=1 ? cos A 2 1 ? cos A 1 ? cos Acos(A 2)=1 ? cos A 2tan(A 2)=1 ? cos A 1 ? cos Acot()=tan(A 2)=1 ? cos A sin A=sin A 1 ? cos A和差化积 sina+sinb=2sina ? b 2cosa ?b 2 a ?b 2sina-sinb=2cosa ? b 2sina ?b 2 a ?b 2cosa+cosb = 2cosa ? b 2coscosa-cosb = -2sina ? b 2sintanA+tanB=sin(A+B)/cosAcosBtanA-tanB=sin(A-B)/cosAcosBctgA+ctgB=sin(A+B)/sinAsinB -ctgA+ctgB=sin(A+B)/sinAsinB积化和差 sinasinb = sinacosb = 诱导公式 sin(-a) = -sina cos(-a) = cosa sin(?2 1 2 1 2[cos(a+b)-cos(a-b)] [sin(a+b)+sin(a-b)]cosacosb = cosasinb =1 2 1 2[cos(a+b)+cos(a-b)] [sin(a+b)-sin(a-b)]?2-a) = cosacos(-a) = sinasin(?2+a) = cosacos(?2+a) = -sinasin(π-a) = sinasin a cos acos(π-a) = -cosasin(π+a) = -sina 万能公式2 tan a 2 a 2cos(π+a) = -cosa tgA=tanA =1 ? (tana 2 a 2) )22 tana 2 a 2sina=1 ? (tancosa=)2tana=21 ? (tan1 ? (tan)2其它公式 a?sina+b?cosa=(a2? b )2 2×sin(a+c) [其中 tanc=2b a]a ba?sin(a)-b?cos(a) = 1+sin(a) =(sin 1-sin(a) = (sina 2 a 2 1 sin a(a? b )×cos(a-c) [其中 tan(c)=]+cos -cosa 2)2 a 2)2 1 cos a其他非重点三角函数 csc(a) = 双曲函数 sinh(a)=e -e 2a -asec(a) =cosh(a)=ea? e 2-atg h(a)=sinh( a ) cosh( a )公式一： 设 α 为任意角三角公式，终边相同的角的同一三角函数的值相等： sin（2kπ＋α）= sinα cos（2kπ＋α）= cosα tan（2kπ＋α）= tanα cot（2kπ＋α）= cotα 公式二： 设 α 为任意角三角公式，π+α 的三角函数值与 α 的三角函数值之间的关系： sin（π＋α）= -sinα cos（π＋α）= -cosα tan（π＋α）= tanα cot（π＋α）= cotα 公式三： 任意角 α 与 -α 的三角函数值之间的关系： sin（-α）= -sinα cos（-α）= cosα tan（-α）= -tanα cot（-α）= -cotα 公式四： 利用公式二和公式三可以得到 π-α 与 α 的三角函数值之间的关系： sin（π-α）= sinα cos（π-α）= -cosα tan（π-α）= -tanα cot（π-α）= -cotα 公式五： 利用公式-和公式三可以得到 2π-α 与 α 的三角函数值之间的关系：sin（2π-α）= -sinα tan（2π-α）= -tanα 公式六：?2cos（2π-α）= cosα cot（2π-α）= -cotα±α 及?23? 2±α 与 α 的三角函数值之间的关系： cos（ cot（ cos（?2sin（ tan（ sin（ sin（ tan（ sin（ tan（+α）= cosα +α）= -cotα -α）= cosα +α）= -cosα +α）= -cotα -α）= -cosα -α）= cotα?2+α）= -sinα +α）= -tanα tan（?2?2?2?2-α）= sinα3? 2 3? 2 3? 2-α）= cotαcot（?2-α）= tanα3? 2 3? 2 3? 2 3? 2cos（ cot（ cos（ cot（+α）= sinα +α）= -tanα -α）= -sinα3? 2-α）= tanα(以上 k∈Z) 正弦定理 余弦定理 正切定理 a/sinA=b/sinB=c/sinC=2R 注： 其中 R 表示三角形的外接圆半径 b2=a2+c2-2accosB 注：角 B 是边 a 和边 c 的夹角 [(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}s in x cos x正切函数 ta n x ? 正割函数 s e c x ?；余切函数 c o t x ? ；余割函数 c s c x ?cos x s in x 1 s in x；1 cos x三角不等式 |a+b|≤|a|+|b| |a-b|≤|a|+|b| |a|≤b<=>-b≤a≤b|a-b|≥|a|-|b| -|a|≤a≤|a| 三角形中的一些结论 (1)anA+tanB+tanC=tanA· tanB· tanC (2)sinA+tsinB+sinC=4cos(A/2)cos(B/2)cos(C/2) (3)cosA+cosB+cosC=4sin(A/2)· sin(B/2)· sin(C/2)+1(4)sin2A+sin2B+sin2C=4sinA· sinB· sinC (5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1反三角函数：a r c s ix n? a r cx c?o s 2?a r c t ax n?a r cx c o t ? 2?a rc sin x ：定义域 [ ? 1,1] ，值域 [ ??2,?2] ； a r c c o s x ：定义域 [ ? 1,1] ，值域 [ 0 , ? ] ；arctan x ：定义域 ( ? ? , ? ? ) ，值域 ( ??2,?2) ； arc co t x ：定义域 ( ? ? , ? ? ) ，值域 ( 0 , ? )式中 n 为任意整数。arc sin x =arc cos x =arc tan x =arc cot x =