勾股定理关于角的特殊定理勾股定理关于：等要三角形直角三角形

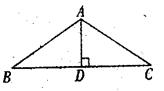
勾股定理证明 利用相似三角形证明

有许多勾股定理的证明方式,都是基于相似三角形中两边长的比例.

设ABC为一直角三角形等腰三角形的顶角为120,直角于角C（看附图）.从点C画上三角形的高,并将此高与AB的交叉点称之为H.此新三角形ACH和原本的三角形ABC相似,因为在两个三角形中都有一个直角（这又是由于“高”的定义）,而两个三角形都有A这个共同角,由此可知第三只角都是相等的.同样道理,三角形CBH和三角形ABC也是相似的.这些相似关系衍生出以下的比率关系：

因为BC=a,AC=b,AB=c

所以a/c=HB/a and b/c=AH/b

可以写成a*a=c*HB and b*b=C*AH

综合这两个方程式,我们得到a*a+b*b=c*HB+C*AH=C*(HB+AH)=c*c

换句话说:a*a+b*b=c*c

[*]----为乘号

欧几里得的证法

在欧几里得的《几何原本》一书中提出勾股定理由以下证明后可成立.设△ABC为一直角三角形,其中A为直角.从A点划一直线至对边,使其垂直于对边上的正方形.此线把对边上的正方形一分为二,其面积分别与其余两个正方形相等.

在正式的证明中,我们需要四个辅助定理如下：

如果两个三角形有两组对应边和这两组边所夹的角相等,则两三角形全等.（SAS定理） 三角形面积是任一同底同高之平行四边形面积的一半.任意一个正方形的面积等于其二边长的乘积.任意一个四方形的面积等于其二边长的乘积（据辅助定理3）.证明的概念为：把上方的两个正方形转换成两个同等面积的平行四边形,再旋转并转换成下方的两个同等面积的长方形.

其证明如下：

设△ABC为一直角三角形,其直角为CAB.其边为BC、AB、和CA,依序绘成四方形CBDE、BAGF和ACIH.画出过点A之BD、CE的平行线.此线将分别与BC和DE直角相交于K、L.分别连接CF、AD,形成两个三角形BCF、BDA.∠CAB和∠BAG都是直角,因此C、A 和 G 都是线性对应的,同理可证B、A和H.∠CBD和∠FBA皆为直角,所以∠ABD等于∠FBC.因为 AB 和 BD 分别等于 FB 和 BC,所以△ABD 必须相等于△FBC.因为 A 与 K 和 L是线性对应的,所以四方形 BDLK 必须二倍面积于△ABD.因为C、A和G有共同线性,所以正方形BAGF必须二倍面积于△FBC.因此四边形 BDLK 必须有相同的面积 BAGF = AB².同理可证,四边形 CKLE 必须有相同的面积 ACIH = AC².把这两个结果相加,AB²+ AC² = BD×BK + KL×KC 由于BD=KL等腰三角形的顶角为120,BD×BK + KL×KC = BD(BK + KC) = BD×BC 由于CBDE是个正方形,因此AB² + AC² = C².此证明是于欧几里得《几何原本》一书第1.47节所提出的

推论：如果a×a+b×b=c×c,则△ABC是直角三角形.如果a×a+b×b>c×c,则△ABC是锐角三角形.如果a×a+b×b＜c×c,则△ABC是钝角三角形.

（1）三角形的角平分线的交点叫做三角形的内心,它是三角形内切圆的圆心,它到各边的距离相等.

（三角形的外接圆圆心,即外心,是三角形三边的垂直平分线的交点,它到三个顶点的距离相等）.

（2）三角形的三条中线的交点叫三角形的重心,它到每个顶点的距离等于它到对边中点的距离的2倍.

（3）三角形的三条高的交点叫做三角形的垂心.

（4）三角形的中位线平行于第三边且等于第三边的1/2.

注意：

① 三角形的内心、重心都在三角形的内部.

② 钝角三角形的垂心、外心在三角形外部.

③ 直角三角形的垂心、外心在三角形的边上.（直角三角形的垂心为直角顶点,外心为斜边中点.）

④ 锐角三角形的垂心、外心在三角形内部.

直角三角形中,角和边的关系公式：

假设这样一个三角形 两条直角边分别为a、b 斜边为c 两直角边的夹角为90度 直角边a与斜边c构成的角为β

则：

当β=30度时 β所对的边（即b）为斜边（即c）的2倍 若设b为1,则c为2,a为 根号下3

当β=45度时 两条斜边（a、b）相等 若设a、b为1,则c为 根号下2

当β=60度时 恰与β=30度时相反