2019中考数学知识点：二次函数与图形变换

二次函数与图形变换

解：y＝2x2－12x＋5＝2(x－3)2－13，顶点坐标为(3，－13)，其图象关于x轴对称的顶点坐标为(3，13)，所以对称后的图象的解析式为y＝－2(x－3)2＋13.。在已知抛物线与x轴两交点的距离和顶点坐标的情况下，问题比较容易解决．由顶点坐标为（3，-2）的条件，易知其对称轴为x＝3，再利用抛物线的对称性，可知图象与x轴两交点的坐标分别为（1，0）和（5，0）。 (3)若题中所给的图形中存在垂直于坐标轴的平面，或点m在坐标轴或坐标平面上，则利用这一条件，再作轴的垂线即可确定点m的坐标． 规律总结：确定空间直角坐标系中任一点p的坐标的步骤是：①过p作pc⊥z轴于点c。

二次函数顶点式ppt：这是一个关于二次函数顶点式ppt，这节课主要是1 会用描点法画出二次函数 的图像2 会说出二次函数图像的开口方向,对称轴,顶点坐标3 培养学生经历由具体到一般的探索事物的规律的过程等等介绍。y=a(x-h)2+k(a≠0,a、h、k为常数),顶点坐标为对称轴为直线x=h，顶点的位置特征和图像的开口方向与函数y=ax2的图像相同，当x=h时，y最值=k。解：y＝2x2－4x＋1＝2(x2－2x＋1)－1＝2(x－1)2－1，该抛物线的顶点坐标是(1，－1)，将其向左平移3个单位，向下平移2个单位后，抛物线的形状，开口方向不变，这时顶点坐标为(1－3，－1－2)，即(－2，－3)，所以平移后抛物线的解析式为y＝2(x＋2)2－3.即y＝2x2＋8x＋5.。

【解析】试题解析：抛物线y=x2先向左平移3个单位，再向上平移1个单位，两次平移后得到的抛物线解析式为：y=x+32+1.。（2）将该抛物线向上平移2个单位长度，再向左平移3个单位长度得到新的二次函数图像，请写出相应的解析式，并用列表，描点，连线的方法画出新二次函数的图像。( 2011,2012)点评:函数y＝ax+2011＋2012的图象恒过定点实际上就是将定点(-2011,2012),实际上就是将定点(0,1)向右平移2011个单位,向上平移2011个单位得到。

分析：将y=x2-2x-3化为顶点式y=(x-1)2-4，a值为1，顶点坐标为(1，-4)，将其图像向上平移2个单位，再向右平移1个单位，那么顶点也会相应移动，其坐标为(2，-2),由于平移不改变二次函数的图像的形状和开口方向，因此a值不变，故平移后的解析式为y=(x- 2)2-2。二次函数图像顶点坐标

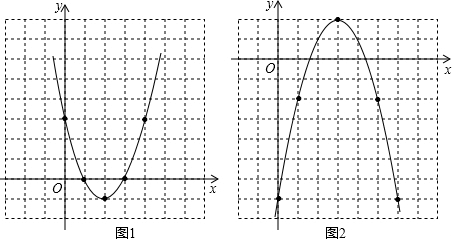
2、轴对称：此图形变换包括x轴对称和关于y轴对称两种方式。

二次函数图像关于x轴对称的图像，其形状不变，但开口方向相反，因此a值为原来的相反数。顶点位置改变，只要根据关于x轴对称的点的坐标特征求出新的顶点坐标，即可确定其解析式。

解：y＝2x2－12x＋5＝2(x－3)2－13，顶点坐标为(3，－13)，其图象关于x轴对称的顶点坐标为(3，13)，所以对称后的图象的解析式为y＝－2(x－3)2＋13.。二次函数顶点式ppt：这是一个关于二次函数顶点式ppt，这节课主要是1 会用描点法画出二次函数 的图像2 会说出二次函数图像的开口方向,对称轴,顶点坐标3 培养学生经历由具体到一般的探索事物的规律的过程等等介绍。y=a(x-h)2+k(a≠0,a、h、k为常数),顶点坐标为对称轴为直线x=h，顶点的位置特征和图像的开口方向与函数y=ax2的图像相同，当x=h时，y最值=k。

例2.求抛物线y=x2-2x-3关于x轴以及y轴对称的抛物线的解析式。

分析：y=x2-2x-3=(x-1)2-4，a值为1，其顶点坐标为(1，-4)，若关于x轴对称，a值为-1，新的顶点坐标为(1，4)，故解析式为y=-(x-1)2+4；若关于y轴对称，a值仍为1，新的顶点坐标为(-1，-4)，因此解析式为y=(x+1)2-4。

二次函数顶点式ppt：这是一个关于二次函数顶点式ppt，这节课主要是1 会用描点法画出二次函数 的图像2 会说出二次函数图像的开口方向,对称轴,顶点坐标3 培养学生经历由具体到一般的探索事物的规律的过程等等介绍。（2）根据题意可判断出一次函数的图象与二次函数的图象交点的横坐标分别为1和，代入二次函数解析式可求出交点坐标，代入一次函数解析式可得出k与n的值，继而得出一次函数解析式．（3）先根据抛物线的开口向上可知a＞0，由顶点纵坐标为－3得出b与a关系，再根据一元二次方程2ax+bx+q=0有实数根可得到关于q的不等式，求出q的取值范围即可．解答：解：（1）由二次函数的图象可知：二次函数的顶点坐标为（1，－3），∵二次函数的对称轴方程为x=1，∴二次函数与x轴的交点坐标为（0，0），（2，0），于是得到方程组，。y=a(x-h)2+k(a≠0,a、h、k为常数),顶点坐标为对称轴为直线x=h，顶点的位置特征和图像的开口方向与函数y=ax2的图像相同，当x=h时，y最值=k。

例3.将抛物线y=x2-2x+3绕其顶点旋转180°，则所得的抛物线的函数解析式为________

分析：y=x2-2x+3=(x-1)2+2中，a值为1，顶点坐标为(1，2)，抛物线绕其顶点旋转180°后，a值为-1，顶点坐标不变，故解析式为y=-(x-1)2+2。

中考声明：该文观点仅代表作者本人，搜狐号系信息发布平台，搜狐仅提供信息存储空间服务。