勾股定理是一条古老的数学定理.它有很多种证明方法．(1)请你(2)

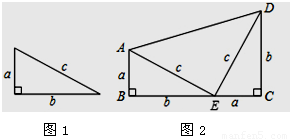
[尝试证明]以图（1）中的直角三角形为基础可以构造出以a、b为底，以a＋b为高的直角梯形如图（2）。请你利用图（2）验证勾股定理；

[知识拓展]利用图(2)的直角梯形，我们可以证明，其证明步骤如下：

∵BC＝a＋b，AD＝.

又∵在直角梯形ABCD中有直角腰BC斜腰AD（填“＞”，“＜”或“＝”），即。

∴

查看答案和解析>>

『问题情境』勾股定理是一条古老的数学定理，它有多种证明方法，我国汉代数学家赵爽根据弦图，利用面积法进行了证明．著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球，作为地球人与其它星球“人”进行第一次“谈话”的语言．

『定理表述』请你根据图1中的直角三角形叙述勾股定理(用文字及符号语言叙述)．

勾股定理的逆定理教学目的知识与技能1、理解勾股定理的逆定理的证明方法并能证明勾股定理的逆定理.2、掌握利用勾股定理的逆定理，并能利用其判定一个三角形是否是直角三角形.过程与方法1、通过对勾股定理逆定理的探索，经历知识的发生、发展与形成的过程.2、通过用三角形三边的数量关。我国古代数学家们不仅很早就发现并应用了勾股定理,而且很早就尝试对勾股定理作出理论性的证明.最早对勾股定理进行证明的,是三国时期吴国的数学家赵爽.他创制了一幅“勾股圆方图”,用形数结合的方法,对勾股定理进行了详细的证明.在“勾股圆方图”中,以弦为边长得到正方形abde,它是由4个相等的直角三角形再加上中间的那个小正方形组成的.每个直角三角形的面积为ab/2。实际上,在更早期的人类活动中,人们就已经认识到这一定理的某些特例．除我国在公元前1000多年前发现勾股定理外,据说古埃及人也曾利用“勾三股四弦五”的法则来确定直角．但是,这一传说引起过许多数学史家的怀疑．比如,美国的数学史家m·克莱因教授曾经指出：“我们也不知道埃及人是否认识到毕达哥拉斯定理．我们知道他们有拉绳人（测量员）,但所传他们在绳上打结,把全长分成长度为3、4、5的三段,然后用来形成直角三角形之说,则从未在任何文件上得到证实．”不过,考古学家们发现了几块大约完成于公元前2000年左右的古巴比伦的泥版书,据专家们考证,其中一块上面刻有如下问题：“一根长度为30个单位的棍子直立在墙上,当其上端滑下6个单位时,请问其下端离开墙角有多远。

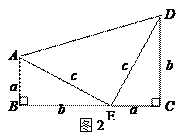
『知识拓展』利用图2中的直角梯形，我们可以证明＜．其证明步骤如下：

∵BC＝a＋b，AD＝，

又在直角梯形ABCD中，BCAD(填大小关系)，

即．

∴＜．

经销商或代理3、 【正确答案】 ：、 【正确答案】 ：c 【答案解析】 ：消费品国际分销渠道的五种模式【答案解析】 ：消费品国际分销渠道的五种模式中，生产者&mdash。* * * * * * 当堂检测 解析答案 则实数m的最大值为________. 解析如图， 当y＝2x经过且只经过x＋y－3＝0和x＝m的交点时，m取到最大值，此时， 即(m,2m)在直线x＋y－3＝0上， 则m＝1. 1 解析答案 解析该不等式组表示的平面区域为如图所示的阴影部分. 故当x＝5，y＝4时，z取得最大值为90. 90 解析答案 解析实数x，y满足的可行域如图中阴影部分所。* * * * * * 解析答案 ∴ac＝3或－8(舍). 解析答案 4.已知锐角三角形的边长分别为1,3，a，则a的范围是. 解析只需让3和a所对的边均为锐角即可. 解析答案 解析由余弦定理得c2＝a2＋b2－2abcos c， ∴a2＋1＋a＝3， 即a2＋a－2＝0， 解得a＝1或a＝－2(舍). 1 解析答案 6.已知△abc的三边长分别为2。