标准差(StandardDeviation)和标准误差(StandardError)

这easy处理：用结果的平方根替代，这样结果就与原来的測量单位一致。

所以上面的样例中的散布程度就是10个IQ点，变得更加easy理解。

最后一个问题是眼下的公式是一个有偏预计，也就是说。结果总是高于或者低于真实的值。

解释略微有点复杂。先要绕个弯。在多数情况下，我们做研究的时候。更感兴趣样本来自的整体（population）。比方，我们探查有年轻男性精神分裂症患者的家庭中的外现情绪（expressedemotion。EE)水平时，我们的兴趣点是全部满足此条件的家庭（整体）。而不单单是哪些受研究的家庭。

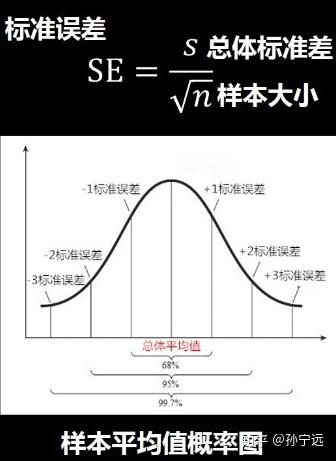
前面的小结中已经多次提到了统计量：小结7中对统计量做了基本说明标准误差 标准差，并且列出了常用的统计量，这些统计量可以用来对总体中的未知参数进行点估计（例如用样本均值估计总体均值）。也就是说，概率$........$当样本大小为n时，样本均值$\bar{x}_n$这个估计量与真值$\theta$的偏离达到$e$这么大或更大的可能性。如果分割后的影像对象平均大小为ｍ 个像素，即从总体中抽取样本容量为ｍ的样本并求 均值，根据式（１），数据集的类内方差与训练样本数 量成正比例关系，对所有均值组成的数据集进行分 类，由于其类内方差为总体方差的Ｉ／ｍ，所要求训练 样本的数量大大减小了。

从同余的概念和上述时钟的例子，不难得出结论：对于某一确定的模，用某数减去小于模的另一个数，总可以用加上“模减去该数绝对值的差”来代替。如果分割后的影像对象平均大小为ｍ 个像素，即从总体中抽取样本容量为ｍ的样本并求 均值，根据式（１），数据集的类内方差与训练样本数 量成正比例关系，对所有均值组成的数据集进行分 类，由于其类内方差为总体方差的Ｉ／ｍ，所要求训练 样本的数量大大减小了。1.理解总体、简单随机样本、统计量、样本均值、样本方差及样本矩的概念，其中样本方差定义为。

标准差(Standard Deviation) 和 标准误差(Standard Error)顺带一下，不要直接使用此公式计算SD，会产生非常多舍入误差(roundingerror)。统计学书通常会提供另外一个等同的公式，能获得更加精确的值。

如今我们完毕了全部推导工作，这意味着什么呢？

假设数据是正态分布的。一旦知道了均值和SD，我们便知道了分值分布的全部情况。对于任一个正态分布，大概2/3（精确的是68.2%）的分值会落在均值-1SD和均值+1 SD之间。95.4%的在均值-2 SD 和均值+2 SD之间。

当已知考生的基本实力（即考生高考分数相对于当年控制线的线差）后标准误差 标准差，它可以告诉我们报考哪些院校比较有把握录取，报考哪些院校有可能录取，报考哪些院校录取的可能性不大，报考哪些院校根本不可能录取。对比近三年我省二本招生院校的分数差（投档分与当年分数线差值）走势，大多数院校处于上升趋势，只有个别院校的分数差趋势忽高忽低。，但我奉劝大家谨慎，因为用两块芯片(最少两块3级或其中一块4、5级或两块都是4、5级的)去合成，那就要谈谈合成成功的概率问题了(游戏的设计者没有公开概率、我已经觉得这有猫腻了、怀疑概率是相当低的)，就以我为例吧，昨天我两次合成都没成功，即便下一次合成成功了，那概率也就是三分之一，也就意味着我已经失去了两块芯片(一块3级一块4级)，这还是基于下次合成成功的基础上所付出的代价，如果你是n次以后才合成成功的，那你就要失去n-1块的芯片,这么多的芯片再加上强化所需的小晶体，那意味这你要付出多么大的代价啊。

总结一下，SD告诉我们分值环绕均值的分布情况。如今我们转向标准误差（standard error）。

标准误差(Standard Error)

如果为 true 或省略，则返回近似匹配值，也就是说，如果找不到精确匹配值，则返回小于 lookup_value 的最大数值。e s 具体计算见伸长值计算表 5.2 实际伸长值计算 实际伸长值 △l1 =△l1 +△l 2 △l 1 --从初应力至最大张拉力间的实际伸长值(mm) △l 2 -初应力下推算伸长值(mm),可采用相邻级的伸长值(采用 15%&delta。在财经日历上，每月公布的非农数据都包含前值、预期值和实际公布值三项数值。

我们可以看到，对于天气来说，只需要统计出以前各种天气独立出现的概率，然后使用全概率公式计算即可，这个道理同样可以用于分词统计上，即根据每个词以前独立出现的概率，计算出整个句子出现的概率。至于概率论，我就笑了，会算概率的人都明白，概率和什么有关，概率是个理论上的抽象东西，是通过理论算出来的（切记是理论上推出的），而不是通过对事件结果统计得出的（大家常见的误区，统计发生过的结果得出的是所占比例而不是下一次的概率，比例和概率有时候是相同的有时候不同，此种情况下是不同的）。两周这样操作下来，通常情况下都会至少有几百上千的真实流量，在这期间，流量上来了，但是真实转化没有，建议要看下宝贝的内功做的如何了，要不然，有流量，没有转化，操作是没有意义的。

）

根据上述统计结果可以大致得出：远视眼的视力在vr实验中得到了一定程度的矫正（这仅仅针对初始视力小于1.5的样本集、并未包含初始视力1.5的样本）。至于概率论，我就笑了，会算概率的人都明白，概率和什么有关，概率是个理论上的抽象东西，是通过理论算出来的（切记是理论上推出的），而不是通过对事件结果统计得出的（大家常见的误区，统计发生过的结果得出的是所占比例而不是下一次的概率，比例和概率有时候是相同的有时候不同，此种情况下是不同的）。a的补事件(戒称逆事件)，记为a 是样本空间中所有丌属亍事件a的样本点的集合aaaa aapp((aa)=1 pp((aa))性质6：相互包含事件的概率差 若事件a包含事件b，则事件a不事件b的差的概率等亍两个 事件概率的差，即： 第一节概率基础 第六章 第六章 概率与概率分布 概率与概率分布 【例】设某地有甲、乙两种报纸，该地成年人中有20%读甲报纸，16%读乙报纸， 8%两种报纸都读。

假设每一个样本是随机的，我们就能够安心地说真实的（整体）均值90%或者95%会落在这个范围内。

我们给这些均值预计的标准差取一个新名字：均值的标准误差（the standard error of themean），缩写是SEM,或者。假设不存在混淆。直接用SE代表。

可是首先得处理一个小纰漏：反复研究（实验）几百次。

现今做一次研究已经非常困难了，不要说几百次了（即使你能花费整个余生来做这些实验）。好在一向给力的统计学家们已经想出了基于单项研究（实验）确定SE的方法。

让我们先从直观的角度来讲：是哪些因素影响了我们对预计精确性的推断？一个明显的因素是研究的规模。样本规模N越大。反常数据对结果的影响就越小，我们的预计就越接近整体的均值。所以，N应该出如今计算SE公式的分母中：由于N越大，SE越小。

相似的。第二因素是：数据的波动越小，我们越相信均值预计能精确反映它们。所以，SD应该出如今计算公式的分子上：SD越大。SE越大。因此我们得出以下公式：

标准差(Standard Deviation) 和 标准误差(Standard Error)

(为什么不是N?

由于实际是我们是在用N除方差SD2，我们实际不想再用平方值。所以就又採用平方根了。)

所以，SD实际上反映的是数据点的波动情况。而SE则是均值的波动情况。

置信区间(Confidence Interval)

前面一节。针对SE，我们提到了某个值范围。我们有95%或者99%的信心觉得真实值就处在其中。我们称这个值范围为“置信区间”，缩写是CI。让我们看看它是怎样计算的。

看正态分布表，你会发现95%的区域处在-1.96SD 和+1.96 SD 之间。

回想到前面的GRE和MCAT的样例。分数均值是500。SD是100，这样95%的分数处在304和696之间。

第二次替代单价因素，以730替代710， 并保留上次替代后的值， 630*730*1.04=478296元 第三次替代损耗率因素，以1.03替代1.04，并保留上两次替代后的值， 630*730*1.03=473697元 （3）计算差额：第一次替代与目标数的差额=465192-443040=22152元 第二次替代与第一次替代的差额=478296-465291=13104元 第三次替代与第二次替代的差额=473697-478296= —4599元。③ 根据附“智能数字显示控制仪说明书”第8页，设置上上限报警值“ahh”（即实际运用中利用上上限报警值替代上限报警值）设置下下限报警值“all”（即实际运用中利用下下限报警值替代下限报警值）。说完上限我们来谈谈下限：和上限不同的是下限防御呈现稳定表现且大多防御系数在1100~1500左右也就是说无论你的防御体现格挡在上限还是下限对方的3000攻至少能减去3分之1的伤害。

所以计算95%的CI的公式是：95%CI= 均值± ( 1.96 xSE)。

选择SD, SE和CI

好了。如今我们有SD,SE和CI。问题也随之而来：什么时候用？选择哪个指标呢？非常明显。当我们描写叙述研究结果时。SD是必须报告的。依据SD和样本大小，读者非常快就能获知SE和随意的CI。假设我们再加入上SE和CI，是不是有反复之嫌？回答是：“YES”和“NO”兼有。

本质上，我们是想告之读者通常数据在不相同本上是存在波动的。

本书通过大量的研究，得出一个很有意思的结论：直到现在为止，没有任何一个经济体可以避免金融波动以及金融崩溃。》——“关于空气污染物的很多研究，例如，究竟多大程度的污染会对人体造成明确伤害，这些物质彼此之间的关系会如何影响它们对生物的效应，这些伤害会不会相互叠加……都还没有明确的结论。对房地产业增加值，《深圳房地产波动规律研究》课题组对其变化规律进行了定量的分析，得出一些规律性的结论：。

某种程度上来讲。这就是检验的显著程度。P level 越低。结果的偶然性就越低。下次能反复出相似结果的可能性越高。

可是显著性检验。一般是黑白分明的：结果要么是显著的，要么不是。

样本数量足够多,再细微的差异都有可能是显著,显著与否与r方大小没有任何关系.r方是说明模型是否较好地拟合了原始数据.换句话说,r方用于评估通过模型预测能在多大程度上还原原始数据的形态,p-value同于评估使用此模型是否与零假设(通常为无模型,即假设自变量与因变量无关系)更好地还原原始数据.总体显著 ...。假设一定的数据集（一定分 布的总体），已知该分布的期望和方差，从这个总 体中抽出一部分（ｍ个）数据，构成一个样本，计算 出一个样本平均值，这样有放回的无数次抽选样 本，将会产生无数个样本平均数，而且这些样本平 均数具有自己的分布形式。中值、中点是统计中常用的方法，用来在大批量样本或者离散性不强的样本间寻找其共性区间，从中点盘运用的对象来讲，这种方式显然不利于反应2个样本间的特质和用来揭示他们的问题，当然不同用法的情况下，这种效果还是可以体现的，比如将个体本命盘与中点盘进行比较，来衡量其差异性，讨论其达到同性标准所需要面对多大的困难，在这样的方法基础上，组合中点盘或者时空中点盘都是代表了一种共体特质标准假设，也就是建立在中点观点基础上的标准假设。

我们会在图表上加上errorbar（误差条，非常难听），通常等同于1个SE。优点是不用选择SE或者CI了（它们指向的是一样的东西），也无过多的计算。不幸的这样的方法传递了非常少实用信息。一个errorbar (-1 SE,+1 SE)等同于68%的CI；代表我们有68%的信心真的均值（或者2个实验组的均值的区别）会落在这个范围内。糟糕的是，我们习惯用95%，99%而不是68%。所以让忘记加上SE吧。传递的信息量太少了，它的主要用途是计算CI。

那么把error bar加长吧，用2个SE怎样？这好像有点意思。2是1.96的不错预计。

有双方面的优点。首先这种方法能显示95%的CI。比68%更有意义。其次能让我们用眼睛检验区别的显著性（至少在2个实验组的情况下是如此）。假设以下bar的顶部和上面bar的底部没有重叠。两个实验组的差异必然是显著的（5%的显著水平）。

因此我们会说。这2个组间存在显著区别。假设我们做t-test，结果会验证这个发现。

这样的方法对超过2个组的情况就不那么精确了。由于须要多次比較（比方。组1和组2。组2和组3，组1和组3），可是至少能给出区别的粗略指示。在表格中展示CI的时候，你应该给出确切的数值（乘以1.96而不是2）。

总结

对任意分布的总体ｊ，期望为ＥＸ，方差为ＤＸ， 有放回抽选样本，容量为ｍ，设样本均值为随机变量 其中，茗。因 此，样本均值数据的分布形式可以很好地近似正态 分布，这样，训练样本数量计算公式的前提条件可以 得到满足。关于数据的检验分析，主要有:z检验(适用于大样本容量的显著性检验，即容量大于30，它是用正太分布理论来推论差异发生的概率，从而判断两个样本平均数的差异是否显著或者判断样本与总体平均数的差异是否显著)。

CI是显著性检验的补充，反映的是真实的均值或者均值区别的范围。

一些期刊已把显著性检验抛弃了，CI取而代之。这可能走过头了。

由于这两种方法各有优点。也均会被误用。

从表4-3也可以看出，就非正常视力的样本而言，vr组在实验中视力下降的比例与平板组较为接近。实验中的另一个观察到的现象是：从实验刚开始到休息结束后，vr组被试中视力持平或者升高发生的比例与平板基本持平，甚至更高，但并未达到统计学意义的显著区别。d 组p-jnk 在1 h 时和a 组比较无显著差异（p ＞0.05 ），但比同时点b 组低（p＜0.05 ），2 h 时也比同时点的c 组（p ＜0.05 ）和b 组（p ＜0.01 ）低，3 h 时点的jnk 磷酸化水平比同时点的c 组（p ＜0.05 ）和b 组（p ＜0.01 ）更低，4 h 时的p-jnk水平与c 组已无显著差异（p ＞0.05 ），却仍高于a 组（p ＜0.05 ），但低于b 组 （p ＜0.05 ）。

与之相反，大量鼓吹的被二手烟影响的人数，实际上不是一个均值预计。

最好的预计是0，它有非常宽的CI。报道的却仅仅是CI的上限。

总之，SD、显著性检验，95%或者99%的CI，均应该加在报告中，有利于读者理解研究结果。它们均有信息量。能相互补充，而不是替代。

相反，“裸”的SE的并不能告诉我们什么信息，多占领了一些篇幅和空间而已。

测量中,为衡量被测点,线,面的尺寸和位置精度而选作依据的点,线,面称为测量基准.一般情况下,多以定位基准作为测量基准.如图5-3所示的容器接口Ⅰ,Ⅱ,Ⅲ都是以m面为测量基准,测量尺寸h1,h2和h2,这样接口的设计标准,定位标准,测量标准三者合一,可以有效地减小装配误差.。而水体类别类 内方差小，分类精度随着样本数量的增加，很快进入 平稳阶段，而且水体在较少的波段数目时（２个）分 类精度明显高于其他类别，说明了数据的复杂程度 对样本数目选择存在显著的影响。5.“掌握正态总体的抽样分布：样本均值、样本方差、样本矩、样本均值差、样本方差比的抽样分布”改为“掌握正态总体的样本均值、样。