傅里叶变换的意义是什么？

傅里叶变换或拉普拉斯变换就是对各向量做傅里叶变换和拉普拉斯变换，得到系统的频响函数矩阵或传递函数矩阵，然后进行傅里叶逆变换或拉普拉斯逆变换得到系统的响应。【注2】对于一些不能直接使用格林公式的被积表达式，借助被积函数积分定义在积分曲线上，满足描述积分曲线的方程，通过描述积分曲线的方程，变换、化简被积表达式，即可以起到化简计算的目的，也可能通过变换使得被积函数符合格林公式的条件，进而可以考虑使用格林公式来计算曲线积分。h ω 是系统单位冲激 响应 的傅利 叶变换 , 称为系统的传递 函数 , x ω 一般它是 ω的复函数 , 可表示为 j φ ω h ω | h ω | e 2 .11 .8 | h ω | 称作系统的幅度。

一般说来，积分变换具有以下的形式（参见维基百科）：

其中 就是积分变换的核 (kernel)。这个积分变换的“物理含义”就是， 在核函数的复共轭这一组正交基上的展开系数。为什么呢？如果大家学过一点线性代数，就可以发现积分变换具有内积的形式。将 看作参数，如果 和 正交，则积分变换无非是给出了向量 在基函数   上投影 / 分量的通式。要注意的是，这里的基函数不是 而是 。这是因为，内积的结果是一个“数”而不是向量，所以作为向量的两个被乘函数必须有一个要被取复共轭（相当于转置）。以上推理从内积的狄拉克括号表示的角度看很容易理解：  ——左矢括号 自带转置效果，要符合原定义则 bra 内必须是 。

在以上的讨论中我提到了向量 ，那它与函数 又是什么关系呢？不妨想象一下普通空间的三维矢量 ，其中的 也无非是向量 在  基矢上的展开系数。也就是说，我们可以通过写出一个矢量在所有基矢量方向的展开系数以及所有基矢量的方式完全确定一个向量。如果把任何一个函数的自变量的任意一个（或者一组，对于多元函数来说）可能的取值看作一个基矢，函数值看作展开系数，那么，任何函数都可以看作是一个向量的一个具体表示。当然了，如果仔细推导一下，函数 的一组正交基实际上是 （狄拉克  函数）。

总结一下，

函数   是向量 在基矢 上的展开系数。

其它任何一组正交函数也可以作为基矢量。

向量 在基矢 的展开系数就是积分变换 。也就是说， 是 的另一表示。

并会区分平行向量、相等向量和共线向量.教学重点:理解并掌握向量、零向量、单位向量、相等向量、共线向量的概念,会表示向量.教学难点:平行向量、相等向量和共线向量的区别和联系.。直观来看就是把0和1当成两个向量，一个量子比特可以是0和1这两个向量的所有可能的组合。本节课是一节概念课,在向量基本概念的形成过程中,需要将学生已有的旧知识作为新知识的固着点和生长点,在探究向量的几何表示时让学生经历以物理中学习力的图示,位移的表示,速度的表示为起点,归纳并确定向量的几何表示以及符号表示,而在探索向量间的特殊关系时,引导学生借助图形进行,这样不仅使研究有序,同时更锻炼学生的直观想象能力,有助于感受向量集数与形于一身的特性。

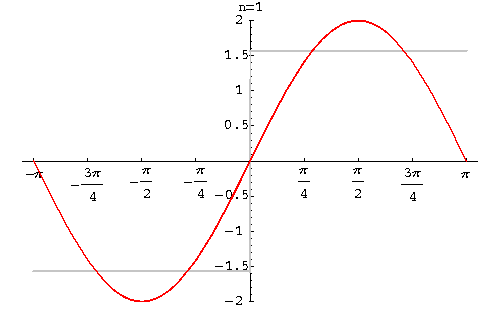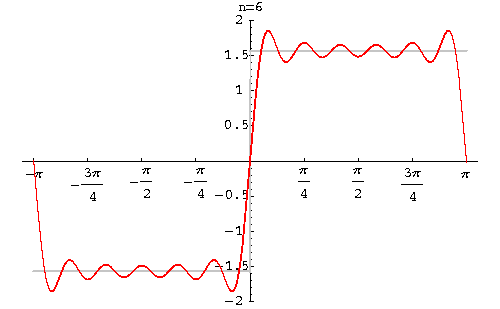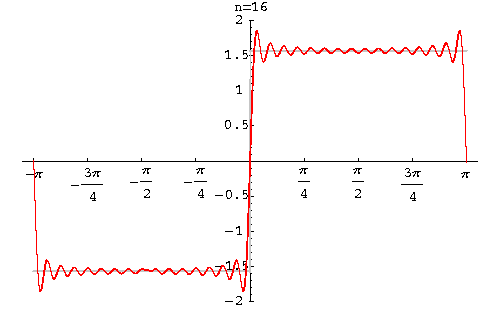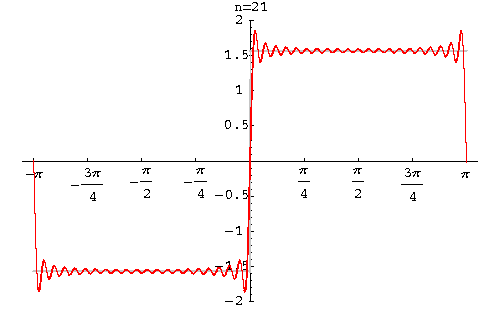
以上的解释仍然比较抽象。实际上，以上述观点进行的傅立叶变换在量子力学中似乎特别多见。如果只限定在薛定谔绘景中讨论，我觉得主要原因是：

量子力学中最神秘的就是叠加态，而“量子纠缠”正是多粒子的一种叠加态。任务之一：研究量子纠缠量子力学中最神秘的就是叠加态，而“量子纠缠”正是多粒子的一种叠加态。任务之一：研究量子纠缠量子力学中最神秘的就是 叠加态，而“量子纠缠”正是多粒子的一种叠加态。

含时薛定谔方程的形式解是复指数函数的形式。而复指数函数正好是复数傅立叶变换的核。

任何其他一阶偏微分算符的本征函数也是复指数函数的形式，而一阶偏微分算符在量子力学中很常见（比如动量算符）。

长程量子纠缠是一个全新的物理现象，它可以导出一大类新的物质态。其过程如下：事先构建一对具有纠缠态的光量子，将这对光量子分别放在通信双方，把具有未知量子态的光量子与发送方的光量子进行联合测量，则接收方的光量子瞬间变化为某种状态，这个状态与发送方的光量子变化后的状态是对称的，然后把联合测量的信息通过经典信道传送给接收方，接收方根据接收到的信息对变化的光量子进行幺正变换（相当于逆转变换）阶越函数的傅立叶变换，就可得到与发送方完全相同的未知量子态。图一，量子反常霍尔效应的示意图，拓扑非平庸的能带结构产生具有手征性的边缘态，从而导致量子反常霍尔效应。

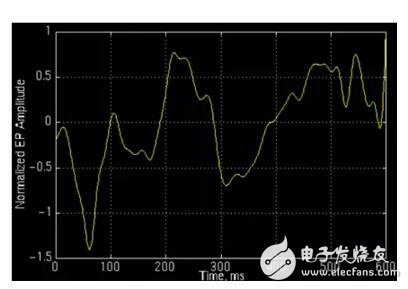
真空态具有有可能存在的最低能量水平，这也是量子场的稳定条件。把真空的能量定为零的经典物理学，无法________一种比真空具有更少能量的物质， 而在量子理论中，真空不再是________，每时每刻都有大量的虚粒子对(一种永远不能直接检测到、但其存在确实具有可测量效应的粒子)产生和湮灭。有暗物质暗能量，真空由量子q组成，它又组成于一对左、右手性的真空态基元，它们在组成q时相互传播的也就是电场行为。

进一步假设 基本不随 变化（相对于指数部分来说阶越函数的傅立叶变换， 时这似乎很合理。这好像就是旋转波近似），则 和 都可以忽略掉——只不过最后有个常系数而已，不影响线型（总归要归一化嘛）。于是我们就可以以 为基函数展开 ，这样我们就得到能量表象中的波函数为 :

∞ - 1 1 j ωt j ω t f [2πδ ω- ω ] 2πδ ω- ω e d ω e 0 0 ∫ 0 2π - ∞ ∞ - 1 1 j ωt - j ω t f [2πδ ω+ ω ] 2πδ ω+ ω e d ω e 0 0 ∫ 0 2π - ∞ 5 若 Φ t 在 t t0 存在 n 阶导数 , 则 ∞ n n n Φ t δ t - t d t - 1 Φ t 2 .6 .10 ∫ 0 0 - ∞由式 2 . 6 . 10 可得 ·13 · 通 信 原 理 ∞ Φ t δ′ t - t d t - Φ′ t 2 .6 .11 ∫ 0 0 - ∞2 . 7 功率信号的傅利叶变换 按照经典数学函数的定义, 功率信号的傅利叶变换是不存在的, 但如果扩大函数定义范围, 引入广义函数 δ t , 则可 以求得功率信号的傅利 叶变换。h ω 是系统单位冲激 响应 的傅利 叶变换 , 称为系统的传递 函数 , x ω 一般它是 ω的复函数 , 可表示为 j φ ω h ω | h ω | e 2 .11 .8 | h ω | 称作系统的幅度。常数项级数的收敛与发散的概念 收敛级数的和的概念 级数的基本性质与收敛的必要条件 几何级数与 级数及其收敛性 正项级数收敛性的判别法 交错级数与莱布尼茨定理 任意项级数的绝对收敛与条件收敛 函数项级数的收敛域与和函数的概念 幂级数及其收敛半径、收敛区间(指开区间)和收敛域 幂级数的和函数 幂级数在其收敛区间内的基本性质 简单幂级数的和函数的求法 初等函数的幂级数展开式 函数的傅里叶(fourier)系数与傅里叶级数 狄利克雷(dirichlet)定理 函数在 上的傅里叶级数 函数在 上的正弦级数和余弦级数。

最后， 在能量表象中的概率分布也就是光谱线型。同样不考虑归一化因子，线型就是：

也就是洛伦兹线型，有的地方又称之为 Breit-Wigner 线型。

Bottom Line: 傅立叶变换（不管正、逆）作为积分变换的一个特例，无非就是求一个向量在一组正交基函数中的展开系数，或者说一个向量在一组给定正交基中的表示。不用硬记变换的时候到底是用 还是 ，实际运用时只要记住内积的表达式就好了。

◉知乎日报与知乎的关系。知乎日报和知乎是共生关系。3、知乎日报、读读日报与知乎错综复杂的定位问题。