【每日一题】2.2.2对数函数和性质的教学目标（二）

对数函数的图像和性质，并学习它的简单应用。（2）教学难点探索对数函数的形象和性质。三、教学过程（一）熟悉的背景，介绍新知识到目前为止，我们学到了哪些基本函数？（一个函数，一个二次函数，一个反比例函数，一个指数函数。让我们一起回忆一下我们在研究指数函数及其性质时的想法？（概念，图像，性质，应用）今天我们将学习另一个新函数。首先，请看看这两个生命的例子，我们在研究指数函数的时候已经看过这两个例子了对数函数教案下载，我们再来看看。例1：当某种类型的细胞分裂时，我们以细胞数x为自变量，以细胞分裂数y为函数值。请填写下表。细胞数 2 4 8 x 细胞分裂数 yy16 4y？Log 2 x… …256 8… …x123 和 x (x∈N*) 关系表达式 例 2：对于 1 米长的绳子，第一次剪掉一半的绳子长度，然后剪掉剩下的绳子第二次Half，如果以绳子的剩余长度x为自变量，以绳子被切断的次数y为函数值，请填写下表。

剩余长度 x... 2 3 4y？Log 1 x2… 8 …x 切断绳索的次数 yy1… (x∈N*) 与 x 的关系。通过前两节的学习，我们知道，对数公式对真数的要求是什么？（真实数大于0），那么两个公式x的取值范围是多少？（x>0）（二）师生互动，探索新知识题1） : 这两个公式 Is a function a function? (It is a function. 是否有任何 y 有一个唯一的 x 值与之对应。) 问题 2：函数 y 的共同结构特征是什么？log 2 x 和 y？ log 1 x2? [学习情境预设：学生可以一次性说出这两个函数的共同特点，如果不能说出，老师会用指数函数类比引导他们。】（PPt显示） ①自变量x在真数的位置；②是 数的底数是常数。它们都可以改写为 y? 哈哈。（类比指数函数）？lo gax问题3：在研究过的四类函数中，常量是有限制的，那么函数y的基数a有限制吗？(A?0 和 a?1) 为什么？因为对数和指数可以相互转换，所以常数a的取值范围为：a? 0 和 ? 1 这就是我们今天要学习的新函数，我们给它起了个名字，叫做对数函数。②是 数的底数是常数。它们都可以改写为 y? 哈哈。（类比指数函数）？lo gax问题3：在研究过的四类函数中，常量是有限制的，那么函数y的基数a有限制吗？(A?0 和 a?1) 为什么？因为对数和指数可以相互转换，所以常数a的取值范围为：a? 0 和 ? 1 这就是我们今天要学习的新函数，我们给它起了个名字，叫做对数函数。②是 数的底数是常数。它们都可以改写为 y? 哈哈。（类比指数函数）？lo gax问题3：在研究过的四类函数中，常量是有限制的，那么函数y的基数a有限制吗？(A?0 和 a?1) 为什么？因为对数和指数可以相互转换，所以常数a的取值范围为：a? 0 和 ? 1 这就是我们今天要学习的新函数，我们给它起了个名字，叫做对数函数。那么函数 y 的基数 a 有限制吗？(A?0 和 a?1) 为什么？因为对数和指数可以相互转换，所以常数a的取值范围为：a? 0 和 ? 1 这就是我们今天要学习的新函数，我们给它起了个名字，叫做对数函数。那么函数 y 的基数 a 有限制吗？(A?0 和 a?1) 为什么？因为对数和指数可以相互转换，所以常数a的取值范围为：a? 0 和 ? 1 这就是我们今天要学习的新函数，我们给它起了个名字，叫做对数函数。

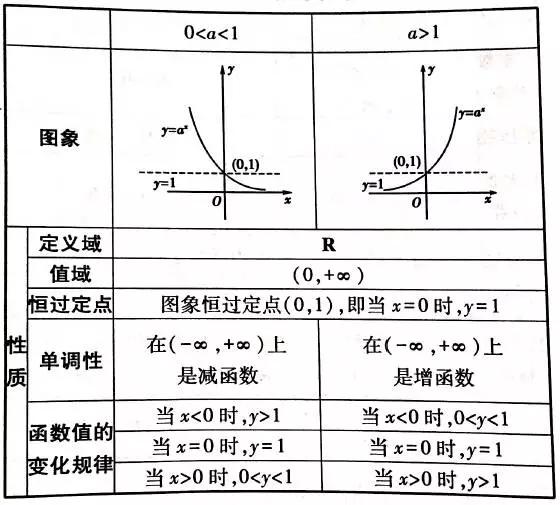
请根据该解析式的结构特点，给出对数函数的一般定义。[对数函数的概念] y 形式的函数？lo gax (a? 0 and a? 1) 称为对数函数，其中 x 是自变量对数函数教案下载，定义域是？0，？？？。练习1、已知对数函数y的图？f (x) 结束 (4, 2）, find f (x). 解决方案： 分析：问题以对数函数形式给出，我们已经了解了对数函数的结构，因此，我们使用该方法待解的未定系数，对数函数中只有一个未知数，所以只有一个方程就足够了。从已知，让 f (x)? Lo gax (a? 0 和 a? 1) ?Y?F(x) 结束 (4, 2）？2 = 洛加 4？一种？42a？2 还是一个?? 2（拒绝）？F(x) ? log 2 x (三）模拟指数函数，结合树形探索性质1、研究函数划分：在学习了对数函数的概念后，对我们来说最重要的是研究其性质这类函数 类似于指数函数的研究，我们也可以通过树状组合来研究它的性质。知道，指数函数的底数会影响函数图的形状。因此，我们要分类讨论a，分为a?1和0?分类?师：既然对数公式和指数公式可以转化为彼此，