【期中复习】小学数学必做100题(2020)(2)

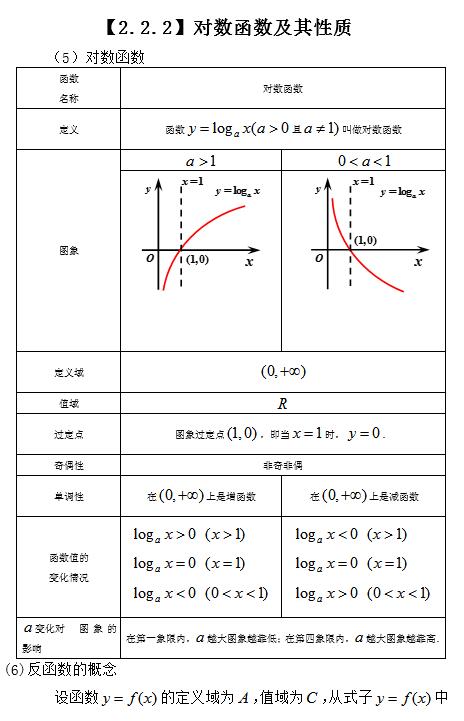
②y=f(x)的像和y=g(x)的像关于直线y=x对称。 ③若y=f(x)的图像通过点(x0,y0,转申请1.(2021福建福州一中中考),已知函数f(x)=logax(a>1 , a≠1) 的图像通过点 (2,3)A.(?3,2)B.(?2,3)C.(3,2)D.(2, 3)答案：C分析：因为函数f(x)=logax，所以函数g(x)=ax的图像经过点2。设a∈R，如果f(x)=log2(x+a) ，反函数的图像通过点( 3,1)A.7B.3C.1D.?1 答案：A 分析：∵f(x)=log2(x+a)∴f(x)=log2 (x+a)∴f(1)=log 解得 a=7。课时评价作业的依据符合标准做法1.（2021浙江杭州高一末）设a=log43,b=log0 .43, c=3A. a>b>c Ba>c> b C. c>a>b D. c>b>a 答案：C 2.（多选）已知函数 f(x) 的图像=logax (a>1, a≠1) 总是穿过点 AA. y=1?x+2 BC y=log22x+1 答案：A; B; C 3. 函数 f(x)=1A. BCD 答案： B 4.（2021年江苏南通高中一中） e 期末) 已知函数f(x)=loga(x+2)+3 的图像总是通过不动点(m,n)，函数g(x)=mx2A.

[1,+∞) B. [?1,+∞) C. (?∞,?1) D. (?∞,1) Answer: B 5. 函数 f(x)=1 +loga(x+2) (a>1, a≠1) 有一个恒定的图像 固定点 A，那么 A 点的坐标；如果 f(?32 答案：(?1,1); 146. (2020)江西南昌师范大学附中）已知函数f(x)为函数y=ax (A>1, a≠1)，且f(9)=?2, then a= Answer: 13 Literacy改进练习7.（多选）若实数a和b满足logaA.0b>1 D .00，loga2b>1，log2a>log2b>0，即1为00，故选ABC。 8.已知函数f(x)=x2+x,?2≤x≤clog12x,c0, 由 f(x) 取值范围为[?1,2]制作图像，如图：当?2≤x ≤c, f(x)=x 由 f(?2)=2, f(1)=2 , F(?1 知道 00,3?2x>0, 解是？所以域函数 y=f(x)?g(x) 是 {x∣?3(2）y=f(x)?g(x) 是一个奇函数。证明 (1）知函数y=f(x)?g(x) 关于原点对称，f(?x)?g(?x)=log 所以函数 y=f(x)?g(x) 是一个奇函数在。创新拓展练习10.让函数y=f(x)和lg((1）求f(x)解析公式和定义域；(2）Find the range of f(x)).

答案：(1）∵lg∴lg∴y=f(x)=10∵y=f(x)和lg(∴x,y应该满足x>0,3?x>0,∴y =f(x) 的定义域为 (0,3). (2）∵3x(3?x)=?3(x?32)2∴y=f(x) 的范围为( 1,10 第二课交互探究对数函数的性质和应用。探究关键能力。解释和细化对数函数的单调性。x>1，∴x的范围是(1,+∞) ).（2）要使函数有意义，1?x解是？10（1）先求g(x)>0解集（即函数f(x)的定义域）。(2）当a>1时，在g(x)>0的前提下，g(x)的单调递增区间是f(x)的单调递增区间，g(x)的单调递减区间是f(x)的递减区间。(3）当0＜a＜1时，在g(x)>0的前提下，g(x)单调递减)递增区间就是f(x)的单调递减区间)，g(x)的单调递减区间就是f(x)的单调递增区间。配给应用 1. 解如下不等式：(1）log1(2）loga 答案：(1）可从题中x>0,4?x>0的含义得到，当解为01时，原不等式等价于2x?5>0,x?1>0，解为x>4；当00，x?1>0时，解为52。综上，当a>1时，原不等式的解集为{x|x>4}；当 0mlog4x 对任何 x∈[4,16] 时，答案：(1）f(x)=(log so t=log4x, when x∈[1,4], y=f(x) = (2t? 2)(t?1=2t=2(t?3) 当t=34时对数函数教案下载，y得到最小值?18，当∴函数取值范围为[?1(2）令k=log4xf( x)>mlog4x 即 2k2?3k+1>mk∴m0, f (x)=log(1）求f(1), f(?1)) 的值; (2）求函数 f (x) 表达式; (3）若f(a?1)?f(3?a)0, 所以 f(x)=?f(?x)=?log 所以 f(x)=lo(3）当 x∈(0,+∞), f(x )=log 令 u=x+7, then y=log 由于 u=x+7 是递增函数，y=log12u 是递减函数，那么因为f(x) 是奇函数，f(0)=0, 所以 y=f(x) 是 R 上的递减函数。

从f(a?1)3?a,解为a>2,即实数a的取值范围为(2,+∞).解题理解综合问题对数函数，常对数函数为依托，重点讲解对数的运算，对数函数的形象和性质，函数的单调性、奇偶性、范围和最大值等，熟悉对数的形象和性质对数函数和求解函数问题 一般规则和方法是回答此类问题的前提 迁移应用 1. 知道函数 f(x)=lg(1）若f(x) 是奇函数，求值a; (2）在(1）的条件下，如果f(x)在(m,n)上的范围是(?1,+∞)，求m和n的值。答案： (1）∵f(x)为奇函数，∴f(x)+f(?x)=0，即lga?x∴(a?x)(a+x)求解a=1（负(2）由（1）知f(x)=lg 那么 1?x1+x 表示 1?x>0,1+x>0 或 1?x0，解为 x> 2 或 t=x2?2x，所以函数f(x)的单调递增区间为(2,+∞)。 4. 求函数f(x)=log 答案：由于判别式x2?3x+5=0，当x∈(?∞)时，判别式∴x2?3x+5>0使得u(x)=x ,32)当x∈(32,+∞)易知y=log∴函数f(x)=log12(x读写逻辑推理-利用对数函数的性质求参数1.已知函数f(x)=lg (1）若函数域为R，求实数a的取值范围；(2）若函数域为R，求实数a的取值范围范围。

答案：（1）如果f(x)的定义域是R，那么不等式ax2+2x+1>0结合二次函数图像（图中省略）给出a>0,22 ?4? a?10，所以实数a的取值范围是[0,1] 识字探索：对数函数域的问题是R，常转化为常数成立问题，再转化为最小值函数的值。值问题，求解问题时，当最高阶项的系数有字母时，需要分类讨论。转应用1.如果函数y=lg(ax2+ax+1)答案: 当a=0, y=lg 当a≠0时，从题意得到a>0，0f(x+2)A.(?53,+∞)C.(?∞,?1) 3)Answer: B 2. (More Optional) 下面关于函数y=lgA. 函数的定义域是(0,+∞) B. 函数的值域是(0,+∞) C.函数在域 D 中单调递增。函数在域中单调递减答案：A；乙; C 3.（2020陕西宝鸡中学一期）若logm3n>1 B.n>m>1 C.00，解为x

教案网123